Thermodynamics is the study of heat, temperature, and their related effects in physical systems. As a subject, thermodynamics is quite complex and expansive, usually taught as a course in itself at universities. The coverage in this book is limited to some of the more elementary and immediately practical facets of thermodynamics rather than a comprehensive overview.
Most people use the words heat and temperature interchangeably. This is unfortunate for every student of thermodynamics, because it means they must first deconstruct this false conception and replace it with one more scientifically accurate before any progress may be made. While “heat” and “temperature” are related concepts, they are not identical.
When people say something is “hot,” what they really mean is that the object has a high temperature. Temperature is a direct function of random molecular motion within an object or a fluid sample. This is usually easiest to visualize for a gas, where unattached molecules have great freedom to vibrate, collide, and otherwise move about. The molecules of a substance at high temperature are moving more vigorously (higher velocity) than the molecules of the same substance at low temperature.
Heat, by contrast, is an expression of thermal energy transfer. By placing a pot of water over a fire, we are adding heat to that pot (transferring thermal energy to the water), the effect of which is to raise its temperature (making the water molecules’ motions more vigorous). If that same pot is taken away from the fire and allowed to cool, its loss of heat (transferring energy out of the water to the surrounding air) will result in its temperature lowering (the individual water molecules slowing down).
Heat gain or loss often results in temperature change, but not always. In some cases heat may be gained or lost with negligible temperature change – here, the gain or loss of heat manifests as physical changes to the substance other than temperature. One example of this is the boiling of water at constant pressure: no matter how much heat is transferred to the water, its temperature will remain constant at the boiling point (100 degrees Celsius at sea level) until all the water has boiled to vapor. The addition of thermal energy to the boiling water does not raise its temperature (i.e. make the molecules move faster), but rather goes into the work of disrupting inter-molecular bonds so that the liquid turns into vapor. Another example is the heating of chemical reactants in an endothermic (heat-absorbing) reaction: much of the thermal energy added to the chemical solution goes into the work of separating chemical bonds, resulting in molecular changes but not (necessarily) increased temperature.
Heat transfer can only happen, though, where there is a difference of temperature between two objects. Thermal energy (heat) naturally flows from the “hotter” (higher-temperature) substance to the “colder” (lower-temperature) substance. To use the boiling water example, the only way to get heat transfer into the water is to subject the water to a hotter substance (e.g., a flame, or a hot electric heating element). If you understand temperature as being molecular motion within a substance, with a hotter object’s molecules vibrating more vigorously than a colder object’s molecules, this natural transfer of heat from hot to cold makes perfect sense: the molecular vibrations of the higher-temperature object literally transfer to the molecules of the lower-temperature object. As those respective molecules touch each other, with fast-vibrating molecules colliding against slow-vibrating molecules, the inter-molecular collisions transfer energy away from the fast-vibrating molecules (so they aren’t vibrating as fast anymore) and toward the slow-moving molecules (so they begin to vibrate faster than before). It’s like a vibrating tuning fork touched to a non-vibrating tuning fork: the vibrating fork loses some of its vibration by transferring energy to the (formerly) quiet tuning fork.
Much more attention will be directed to the concepts of heat and temperature in subsequent subsections.
In an ideal, monatomic gas (one atom per molecule), the mathematical relationship between average molecular velocity and temperature is as follows:
\[{1 \over 2}m\overline{v^2} = {3 \over 2}kT\]
Where,
\(m\) = Mass of each molecule
\(v\) = Velocity of a molecule in the sample
\(\overline{v}\) = Average (“mean”) velocity of all molecules in the sample
\(\overline{v^2}\) = Mean-squared molecular velocities in the sample
\(k\) = Boltzmann’s constant (1.38 \(\times\) 10\(^{-23}\) J / K)
\(T\) = Absolute temperature (Kelvin)
Non-ideal gases, liquids, and solids are more complex than this. Not only can the atoms of complex molecules move to and fro, but they may also twist and oscillate with respect to each other. No matter how complex the particular substance may be, however, the basic principle remains unchanged: temperature is an expression of how rapidly molecules move within a substance.
There is a temperature at which all molecular motion ceases. At that temperature, the substance cannot possibly become “colder,” because there is no more motion to halt. This temperature is called absolute zero, equal to \(-273.15\) degrees Celsius, or \(-459.67\) degrees Fahrenheit. Two temperature scales based on this absolute zero point, Kelvin and Rankine, express temperature relative to absolute zero. That is, zero Kelvin and zero degrees Rankine is equal to absolute zero temperature. Any temperature greater than absolute zero will be a positive value in either the Kelvin or the Rankine scales. A sample of freezing water at sea level, for example, is 0 degrees Celsius (32 degrees Fahrenheit) but could also be expressed as 273.15 Kelvin (0 plus 273.15) or 491.67 degrees Rankine (32 plus 459.67).
A table of melting and boiling points (at sea-level atmospheric pressure) for various substances appears in this table, labeled in these four different units of temperature measurement:
| Melting or boiling substance | $^{o}$C | $^{o}$F & K & $^{o}$R | ||
|---|---|---|---|---|
| Melting point of water (H$_{2}$O) | 0 | 32 | 273.15 | 491.67 |
| Boiling point of water (H$_{2}$O) | 100 | 212 | 373.15 | 671.67 |
| Melting point of ammonia (NH$_{3}$) | $-77.7$ | $-107.9$ | 195.45 | 351.77 |
| Boiling point of ammonia (NH$_{3}$) | $-33.6$ | $-28.5$ | 239.55 | 431.17 |
| Melting point of gold (Au) | 1063 | 1945 | 1336 | 2405 |
| Melting point of magnesium (Mg) | 651 | 1203.8 | 924.2 | 1663.5 |
| Boiling point of acetone (C$_{3}$H$_{6}$O) | 56.5 | 133.7 | 329.65 | 593.37 |
| Boiling point of propane (C$_{3}$H$_{8}$) | $-42.1$ | $-43.8$ | 231.05 | 415.87 |
| Boiling point of ethanol (C$_{2}$H$_{6}$O) | 78.4 | 173.1 | 351.55 | 632.77 |
Note how degrees Celsius and Kelvin for each point on the table differ by a constant (offset) of 273.15, while each corresponding degree Fahrenheit and degree Rankine value differs by 459.67 (note that many of the figures in this table are slightly rounded, so the offset might not be exactly that much). You might think of Kelvin as nothing more than the Celsius scale zero-shifted by 273.15 degrees, and likewise degrees Rankine as nothing more than the Fahrenheit scale zero-shifted by 459.67 degrees.
Note also how increments in temperature measured in degrees Fahrenheit are the same as increments of temperature measured in degrees Rankine. The same is true for degrees Celsius and Kelvin. The difference between the melting point of ammonia (\(-77.7\) degrees C) and the melting point of water (0 degrees C) is the same difference as that between the melting points of ammonia and water expressed in Kelvin: 195.45 and 273.15, respectively. Either way, the difference in temperature between these two substances’ melting points is 77.7 degrees (C or K). This is useful to know when dealing with temperature changes over time, or temperature differences between points in a system – if an equation asks for a temperature difference (\(\Delta T\)) in Kelvin, it is the same value as the temperature difference expressed in Celsius. Likewise, a \(\Delta T\) expressed in degrees Rankine is identical to a \(\Delta T\) expressed in degrees Fahrenheit. This is analogous to differences between two fluid pressures expressed in PSIG versus PSIA: the differential pressure value (PSID) will be the same.
Most people are familiar with the Fahrenheit and Celsius temperature scales used to express temperature in common applications, but the absolute scales of Rankine and Kelvin have special significance and purpose in scientific endeavors. The fact that Rankine and Kelvin are absolute scales in the same manner that atmospheres and torr are units of absolute pressure measurement makes them uniquely suited for expressing temperature (molecular motion) in relation to the absence of thermal energy. Certain scientific laws such as the Ideal Gas Law and the Stefan-Boltzmann Law relate other physical quantities to absolute temperature, and so require the use of these absolute units of measurement.
Heat, being the transfer of energy in thermal (molecular motion) form, may be measured in the same units as any other form of energy is measured: joules (metric) and foot-pounds (British). However, special units of measurement are often used for heat instead:
A calorie of heat is defined as the amount of thermal energy transfer required to change the temperature of one gram of water by one degree Celsius (\(\Delta T\) = 1 \(^{o}\)C = 1 K). One calorie is equivalent to 4.186 joules.
A British Thermal Unit, or BTU is defined as the amount of thermal energy transfer required to change the temperature of one pound of water by one degree Fahrenheit (\(\Delta T\) = 1 \(^{o}\)F = 1 \(^{o}\)R). One BTU is equivalent to 778.2 foot-pounds.
The unit of “dietary” calories is used to express the amount of thermal energy available in a sample of food by combustion. Since the official unit of the “calorie” is so small compared to the typical amounts of energy contained in a meal, nutritionists use the unit of the kilocalorie (1000 calories, or 4186 joules) and call it “Calorie” (with a capital letter “C”).
Just as “Calories” are used to rate the energy content of food, the heat units of “calories” and “BTU” are very useful in describing the potency of various industrial fuels. The following table shows the heat of combustion for a few common fuels, in units of kilocalories per gram and BTU per pound:
| Fuel | Combustion heat (kcal/g) | Combustion heat (BTU/lb) |
|---|---|---|
| Methane (CH$_{4}$) | 13.3 | 23940 |
| Methanol (CH$_{4}$O) | 5.43 | 9767 |
| Ethanol (C$_{2}$H$_{6}$O) | 7.10 | 12783 |
| Propane (C$_{3}$H$_{8}$) | 12.1 | 21700 |
| Carbon monoxide (CO) | 2.415 | 4347 |
For example, if exactly one gram of methane gas were completely burnt, the resulting heat liberated in the fire would be sufficient to warm 13.3 kilograms of water from 20 degrees Celsius to 21 degrees Celsius (a temperature rise, or \(\Delta T\), of one degree Celsius).
If a meal rated at 900 Calories (900 “dietary calories,” or 900 kilocalories) of energy were completely metabolized, the resulting heat would be sufficient to warm a pool of water 900 kilograms in mass (900 liters, or about 237 gallons) by one degree Celsius. This same amount of heat could raise half the amount of water twice the temperature rise: 450 liters of water warmed two degrees Celsius.
Heat spontaneously flows from higher-temperature substances to lower-temperature substances. This is the phenomenon you experience standing next to a fire on a cold day. Your body is cold (low temperature), but the fire is much hotter (high temperature), and your proximity to the fire aids in heat transfer from the fire to you.
Three principal methods exist for heat to transfer from one substance to another:
Practical examples of heat transfer often involve multiple modes rather than just one. For example, the transfer of heat to a person’s body by sunlight obviously involves radiation from the Sun, but it also involves conduction through layers of clothing and convection by air passing from sun-warmed objects to the person.
Temperature-sensing instruments used to measure temperature in industrial applications likewise rely on multiple heat-transfer modes to sample thermal energy from a process fluid or object(s). Infrared thermometers detect temperature by sensing the intensity of infrared light radiated by hot objects. A thermocouple directly touching a hot object relies on conduction to sense the temperature of that object. An RTD inserted into a pipe carrying a hot fluid relies on convection to measure the average temperature of that fluid. A filled-bulb thermometer inserted into a thermowell, inserted into a fluid-filled process vessel relies on both convection (from the process fluid to the thermowell) and conduction (from the thermowell to the bulb) to sense process temperature.
If you have ever experienced the immediate sensation of heat from a large fire or explosion some distance away, you know how radiation works to transfer thermal energy. Radiation is also the method of heat transfer experienced in the Earth’s receiving of heat from the Sun (and also the mechanism of heat loss from Earth to outer space). Radiation is the least efficient of the three heat transfer mechanisms. It may be quantified by the Stefan-Boltzmann Law, which states the rate of heat lost by an object (\(dQ \over dt\)) is proportional to the fourth power of its absolute temperature, and directly proportional to its radiating area:
\[{dQ \over dt} = e \sigma A T^4\]
Where,
\(dQ \over dt\) = Radiant heat loss rate (watts)
\(e\) = Emissivity factor (unitless)
\(\sigma\) = Stefan-Boltzmann constant (5.67 \(\times\) \(10^{-8}\) W / m\(^{2}\) \(\cdot\) K\(^{4}\))
\(A\) = Surface area (square meters)
\(T\) = Absolute temperature (Kelvin)
Here is one of the scientific applications where temperature expressed in absolute units is truly necessary. Radiant energy is a direct function of molecular motion, and so we would logically expect objects to radiate energy at any temperature above absolute zero. The temperature value used in this formula must be in units of Kelvin in order for the resulting \(dQ \over dt\) value to be correct. If degrees Celsius were used for \(T\) instead of Kelvin, the formula would predict zero thermal radiation at the freezing point of water (0 \(^{o}\)C) and negative radiation at any temperature below freezing, which is not true. Remember that the “zero” points of the Celsius and Fahrenheit scales were arbitrarily set by the inventors of those scales, but that the “zero” points of the Kelvin and Rankine scales reflect a fundamental limit of nature.
The emissivity factor varies with surface finish and color, ranging from one (ideal) to zero (no radiation possible). Dark-colored, rough surfaces offer the greatest emissivity factors, which is why heater elements and radiators are usually painted black. Shiny (reflective), smooth surfaces offer the least emissivity, which is why thermally insulating surfaces are often painted white or silver.
Like all heat-transfer modes, radiation is two-way. Objects may emit energy in the form of radiation, and they may also receive energy in the form of radiation. Everyone knows white-colored shirts are cooler than black-colored shirts worn on a hot, sunny day – this is an example of how emissivity affects heat absorption by radiant transfer. A black-colored shirt (high emissivity value) enhances the receiving of radiant energy by your body from the sun. What is not as obvious, though, is that a white-colored shirt will keep you warmer than a black-colored shirt on a cold, dark day because that same decreased emissivity inhibits body heat loss by radiation. Thus, high-emissivity objects both heat and cool more readily by radiation than low-emissivity objects.
If you have ever accidently touched a hot iron or stove heating element, you possess a very vivid recollection of heat transfer through conduction. In conduction, fast-moving molecules in the hot substance transfer some of their kinetic energy to slower-moving molecules in the cold substance. Since this transfer of energy requires collisions between molecules, it only applies when the hot and cold substances directly contact each other.
Perhaps the most common application of heat conduction in industrial processes is through the walls of a furnace or some other enclosure containing an extreme temperature. In such applications, the desire is usually to minimize heat loss through the walls, so those walls will be “insulated” with a substance having poor thermal conductivity.
Conductive heat transfer rate is proportional to the difference in temperature between the hot and cold points, the area of contact, the distance of heat travel from hot to cold, and the thermal conductivity of the substance:
\[{dQ \over dt} = {kA {\Delta T} \over l}\]
Where,
\(dQ \over dt\) = Conductive heat transfer rate
\(k\) = Thermal conductivity
\(A\) = Surface area
\(\Delta T\) = Difference of temperature between “hot” and “cold” sides
\(l\) = Length of heat flow path from “hot” to “cold” side
Note the meaning of “\(\Delta T\)” in this context: it refers to the difference in temperature between two different locations in a system. Sometimes the exact same symbology (“\(\Delta T\)”) refers to a change in temperature over time in the study of thermodynamics. Unfortunately, the only way to distinguish one meaning of \(\Delta T\) from the other is by context.
An illustration showing heat conduction through a wall gives context to the variables in the previous equation. As we see here, \(A\) refers to the surface area of the wall, \(\Delta T\) refers to the difference of temperature between either surface of the wall, and \(l\) refers to the thickness of the wall:

In the United States, a common measure of insulating ability used for the calculation of conductive heat loss in shelters is the R-value. The greater the R-value of a thermally insulating material, the less conductive it is to heat (lower \(k\) value). “R-value” mathematically relates to \(k\) and \(l\) by the following equation:
\[R = {l \over k}\]
Rearranging this equation, we see that \(l = kR\), and this allows us to substitute \(kR\) for \(l\) in the conduction heat equation, then cancel the \(k\) terms:
\[{dQ \over dt} = {kA {\Delta T} \over kR}\]
\[{dQ \over dt} = {A {\Delta T} \over R}\]
\(R\) is always expressed in the compound unit of square feet \(\cdot\) hours \(\cdot\) degrees Fahrenheit per BTU. This way, with a value for area expressed in square feet and a temperature difference expressed in degrees Fahrenheit, the resulting heat transfer rate (\(dQ \over dt\)) will naturally be in units of BTU per hour, which is the standard unit in the United States for expressing heat output for combustion-type heaters. Dimensional analysis shows how the units cancel to yield a heat transfer rate in BTUs per hour:
\[{[\hbox{BTU}] \over [\hbox{h}]} = {[\hbox{ft}^2] [^{o}\hbox{F}] \over {{[\hbox{ft}^2] [\hbox{h}] [^{o}\hbox{F}]} \over [\hbox{BTU}]}}\]
The utility of R-value ratings may be shown by a short example. Consider a contractor trailer, raised up off the ground on a mobile platform, with a total skin surface area of 2400 square feet (walls, floor, and roof) and a uniform R-value of 4 for all surfaces. If the trailer’s internal temperature must be maintained at 70 degrees Fahrenheit while the outside temperature averages 40 degrees Fahrenheit, the required output of the trailer’s heater will be:
\[{dQ \over dt} = {(2400 \hbox{ ft}^2) ({30 ^o \hbox{ F})} \over {4 \hbox{ ft}^2 \cdot \hbox{h} \cdot ^{o}\hbox{F} / \hbox{BTU}}} = 18000 \hbox{ BTU per hour}\]
If the trailer’s heater is powered by propane and rated at 80% efficiency (requiring 22500 BTU per hour of fuel heating value to produce 18000 BTU per hour of heat transfer into the trailer), the propane usage will be just over one pound per hour, since propane fuel has a heating value of 21700 BTU per pound.
Most industrial heat-transfer processes occur through convection, where a moving fluid acts as an intermediary substance to transfer heat from a hot substance (heat source) to a cold substance (heat sink). Convection may be thought of as two-stage heat conduction on a molecular scale: fluid molecules come into direct contact with a hot object and absorb heat from that object through conduction, then those molecules later release that heat energy through conduction by direct contact with a cooler object. If the fluid is recycled in a piping loop, the two-stage conduction process repeats indefinitely, individual molecules heating up as they absorb heat from the heat source and then cooling down as they release heat to the heat sink.
Special process devices called heat exchangers perform this heat transfer function between two different fluids, the two fluids circulating past each other on different sides of tube walls. A simple example of a heat exchanger is the radiator connected to the engine of an automobile, being a water-to-air exchanger, the engine’s hot water transferring heat to cooling air entering the grille of the car as it moves.
Another example of a liquid-to-air heat exchanger is the condenser on a heat pump, refrigerator, or air conditioner, a photograph appearing here:

Another common style of heat exchanger works to transfer heat between two liquids. A small example of this design used to transfer heat from a boat engine is shown here:

The purpose for this heat exchanger is to exchange heat between the liquid coolant of the boat engine and sea water, the latter being quite corrosive to most metals. An engine would soon be damaged if sea water were used directly as the coolant fluid, and so heat exchangers such as this provide a means to release excess heat to the sea without subjecting the engine block to undue corrosion. The heat exchanger, of course, does suffer from the corrosive effects of sea water, but at least it is less expensive and more convenient to replace than an entire engine when it reaches the end of its service life.
This marine engine heat exchanger is an example of a shell-and-tube design, where one fluid passes inside small tubes and a second fluid passes outside those same tubes, the tube bundle being contained in a shell. The interior of such an exchanger looks like this when cut away:

The tubes of this particular heat exchanger are made of copper, a metal with extremely high thermal conductivity (\(k\)), to facilitate conductive heat transfer.
Liquid-to-liquid heat exchangers are quite common in industry, where a set of tubes carry one process liquid while a second process liquid circulates on the outside of those same tubes. The metal walls of the tubes act as heat transfer areas for conduction to occur. Metals such as copper with very high \(k\) values (very low \(R\) values) encourage heat transfer, while long lengths of tube ensure ample surface area for heat exchange.
A common application of liquid-to-liquid heat exchangers is in exothermic (heat-releasing) chemical reaction processes where the reactants must be pre-heated before entering a reaction vessel (“reactor”). Since the chemical reaction is exothermic, the reaction itself may be used as the heat source for pre-heating the incoming feed. A simple P&ID shows how a heat exchanger accomplishes this transfer of heat:

Another industrial application of heat exchangers is in distillation processes, where mixed components are separated from each other by a continuous process of boiling and condensation. Alcohol purification is one example of distillation, where a mixture of alcohol and water are separated to yield a purer (higher-percentage) concentration of alcohol. Distillation (also called fractionation) is a very energy-intensive process, requiring great inputs of heat to perform the task of separation. Any method of energy conservation typically yields significant cost savings in a distillation process, and so we often find heat exchangers used to transfer heat from outgoing (distilled, or fractionated) products to the incoming feed mixture, pre-heating the feed so that less heat need be added to the distillation process from an external source.
The following P&ID shows a simple distillation process complete with heat exchangers for reboiling (adding heat to the bottom of the distillation column), condensing (extracting heat from the “overhead” product at the top of the column), and energy conservation (transferring heat from the hot products to the incoming feed):

Distillation “columns” (also called fractionating towers in the industry) are tall vessels containing sets of “trays” where rising vapors from the boiling process contact falling liquid from the condensing process. Temperatures increase toward the bottom of the column, while temperatures decrease toward the top. In this case, steam through a “reboiler” drives the boiling process at the bottom of the column (heat input), and cold water through a “condenser” drives the condensing process at the top of the column (heat extraction). Products coming off the column at intermediate points are hot enough to serve as pre-heating flows for the incoming feed. Note how the “economizing” heat exchangers expose the cold feed flow to the cooler Product A before exposing it to the warmer Product B, and then finally the warmest “Bottoms” product. This sequence of cooler-to-warmer maximizes the efficiency of the heat exchange process, with the incoming feed flowing past products of increasing temperature as it warms up to the necessary temperature for distillation entering the column.
Some heat exchangers transfer heat from hot gases to cool(er) liquids An example of this type of heat exchanger is the construction of a steam boiler, where hot combustion gases transfer heat to water flowing inside metal tubes:

Here, hot gases from the combustion burners travel past the metal “riser” tubes, transferring heat to the water within those tubes. This also serves to illustrate an important convection phenomenon: a thermal siphon (often written as thermosiphon). As water heats in the “riser” tubes, it becomes less dense, producing less hydrostatic pressure at the bottom of those tubes than the colder water in the “downcomer” tubes. This difference of pressure causes the colder water in the downcomer tubes to flow down to the mud drum, and hot water in the riser tubes to flow up to the steam drum. This natural convection current will continue as long as heat is applied to the riser tubes by the burners, and an unobstructed path exists for water to flow in a loop.
Natural convection also occurs in heated air, such as in the vicinity of a lit candle:

This thermally forced circulation of air helps convect heat from the candle to all other points within the room it is located, by carrying heated air molecules to colder objects.
Earlier, we saw how units of heat measurement were defined in terms of the amount of energy gain or loss required to alter the temperature of a water sample by one degree. In the case of the calorie, it was the amount of heat gain/loss required to heat/cool one gram of water one degree Celsius. In the case of the BTU, it was the amount of heat gain/loss required to heat/cool one pound of water one degree Fahrenheit.
As one might expect, one heat unit might be similarly defined as the amount of heat gain or loss to alter the temperature one-half of a degree for twice as much water, or two degrees for half as much water. We could express this as a proportionality:
\[Q \propto m \Delta T\]
Where,
\(Q\) = Heat gain or loss
\(m\) = Mass of sample
\(\Delta T\) = Temperature change (rise or fall) over time
The next logical question to ask is, “How does the relationship between heat and temperature change work for substances other than water?” Does it take the same amount of heat to change the temperature of one gram of iron by one degree Celsius as it does to change the temperature of one gram of water by one degree Celsius? The answer to this question is a resounding no! Different substances require vastly different amounts of heat gain/loss to alter their temperature by the same degree, even when the masses of those substances happen to be identical.
We have a term for this ability to absorb or release heat, called heat capacity or specific heat, symbolized by the variable c. Thus, our heat/mass/temperature change relationship may be described as a true formula instead of a mere proportionality:
\[Q = mc \Delta T\]
Where,
\(Q\) = Heat gain or loss (metric calories or British BTU)
\(m\) = Mass of sample (metric grams or British pounds)
\(c\) = Specific heat of substance
\(\Delta T\) = Temperature change (metric degrees Celsius or British degrees Fahrenheit)
Pure water, being the standard by which all other substances are measured, has a specific heat value of 1. The smaller the value for \(c\), the less heat gain or loss is required to alter the substance’s temperature by a set amount. That substance (with a low value of \(c\)) has a low “heat capacity” because each degree of temperature rise or fall represents a relatively small amount of energy gained or lost. Substances with low \(c\) values are easy to heat and cool, while substances having high \(c\) values require much heat in order to alter their temperatures, assuming equal masses.
A table of specific heat values (at room temperature, 25 degrees Celsius) for common substances appears here:
| Substance | Specific heat value ($c$) cal/g$\cdot$$^{o}$C or BTU/lb$\cdot$$^{o}$F |
|---|---|
| Aluminum (solid) | 0.215 |
| Iron (solid) | 0.108 |
| Copper (solid) | 0.092 |
| Lead (solid) | 0.031 |
| Ice (solid) | 0.50 |
| Water (liquid) | 1.00 |
| Methanol (liquid) | 0.609 |
| Ethanol (liquid) | 0.587 |
| Acetone (liquid) | 0.521 |
| Hydrogen (gas) | 3.41 |
| Helium (gas) | 1.24 |
| Nitrogen (gas) | 0.249 |
| Oxygen (gas) | 0.219 |
| Steam (gas) | 0.476 |
If a liquid or a gas is chosen for use as a coolant (a substance to efficiently convect heat away from an object), greater values of \(c\) are better. Water is one of the best liquid coolants with its relatively high \(c\) value of one: it has more capacity to absorb heat than other liquids, for the same rise in temperature. The ideal coolant would have an infinite \(c\) value, being able to absorb an infinite amount of heat without itself rising in temperature at all.
As you can see from the table, the light gases (hydrogen and helium) have extraordinarily high \(c\) values. Consequently, they function as excellent media for convective heat transfer. This is why large electric power generators often use hydrogen gas as a coolant: hydrogen has an amazing ability to absorb heat from the wire windings of a generator without rising much in temperature. In other words, hydrogen absorbs a lot of heat while still remaining “cool” (i.e. remains at a low temperature). Helium, although not quite as good a coolant as hydrogen, has the distinct advantage of being chemically inert (non-reactive), in stark contrast to hydrogen’s extreme flammability. Some nuclear reactors use helium gas as a coolant rather than a liquid such as water or molten sodium metal.
Lead has an extraordinarily low \(c\) value, being a rather “easy” substance to heat up and cool down. Anyone who has ever cast their own lead bullets for a firearm knows how quickly a new lead bullet cools off after being released from the mold, especially if that same person has experience casting other metals such as aluminum.
Numerical examples are helpful to better understand specific heat. Consider a case where a copper pot filled with water receives heat from a small gas burner operating at an output of 5000 BTU per hour (350 calories per second):

A reasonable question to ask would be, “How much will the temperature of this water-filled pot rise after 40 seconds of heating?” With the burner’s heat output of 350 calories per second and a heating time of 40 seconds, we may assume the amount of heat absorbed by the water-filled pot will be the simple product of heat rate times time:
\[Q = \left({dQ \over dt}\right) t = \left({350 \hbox{ cal} \over \hbox{s}}\right) 40 \hbox{ s} = 14000 \hbox{ calories}\]
This amount of heat not only goes into raising the temperature of the water, but it also raises the temperature of the copper pot. Each substance (water, copper) has its own specific heat and mass values (\(c\) and \(m\)), but they will share the same temperature rise (\(\Delta T\)), so we must sum their heats as follows:
\[Q_{total} = Q_{pot} + Q_{water}\]
\[Q_{total} = m_{pot}c_{pot} \Delta T + m_{water}c_{water} \Delta T\]
Since both the pot and the water start at the same temperature and end at the same temperature, \(\Delta T\) is a common variable to both terms and may therefore be factored out:
\[Q_{total} = (m_{pot}c_{pot} + m_{water}c_{water}) \Delta T\]
Solving this equation for temperature rise, we get:
\[\Delta T = {Q_{total} \over {m_{pot}c_{pot} + m_{water}c_{water}}}\]
\[\Delta T = {14000 \hbox{ cal} \over {(1100 \hbox{ g})(0.092 {\hbox{cal} \over \hbox{g}^o\hbox{C}}) + (3700 \hbox{ g})(1 {\hbox{cal} \over \hbox{g}^o\hbox{C}})}}\]
\[\Delta T = 3.68 \> ^o\hbox{C}\]
So, if the water and pot began at a temperature of 20 degrees Celsius, they will be at a temperature of 23.68 degrees Celsius after 40 seconds of heating over this small burner.
Another example involves the mixing of two substances at different temperatures. Suppose a heated mass of iron drops into a cool container of water. Obviously, the iron will lose heat energy to the water, causing the iron to decrease in temperature while the water rises in temperature. Suppose the iron’s mass is 100 grams, and its original temperature is 65 degrees Celsius. Suppose the water’s mass is 500 grams, and its original temperature is 20 degrees Celsius:

What will the equilibrium temperature be after the iron falls into the water and both their temperatures equalize? We may solve this by setting two heat equations equal to each other: the heat lost by the iron and the heat gained by the water, with the final equilibrium temperature being \(T\):
\[Q_{iron} = Q_{water}\]
\[m_{iron}c_{iron} \Delta T_{iron} = m_{water}c_{water} \Delta T_{water}\]
\[m_{iron}c_{iron} (65 \> ^o\hbox{C} - T) = m_{water}c_{water} (T - 20 \> ^o\hbox{C})\]
Note how the \(\Delta T\) term is carefully set up for each side of the equation. In order to make the iron’s heat loss a positive value and the water’s heat gain a positive value, we must ensure the quantity within each set of parentheses is positive. For the iron, this means \(\Delta T\) will be 65 degrees minus the final temperature. For the water, this means \(\Delta T\) will be the final temperature minus its starting temperature of 20 degrees.
In order to solve for the final temperature (\(T\)), we must distribute the terms, collecting all \(T\)-containing terms to one side of the equation, then factor and isolate \(T\):
\[m_{iron}c_{iron}(65) - m_{iron}c_{iron}T = m_{water}c_{water}T - m_{water}c_{water}(20)\]
\[m_{iron}c_{iron}(65) + m_{water}c_{water}(20) = m_{iron}c_{iron}T + m_{water}c_{water}T\]
\[m_{iron}c_{iron}(65) + m_{water}c_{water}(20) = T(m_{iron}c_{iron} + m_{water}c_{water})\]
\[T = {{m_{iron}c_{iron}(65) + m_{water}c_{water}(20)} \over {m_{iron}c_{iron} + m_{water}c_{water}}}\]
\[T = {{(100 \hbox{ g})(0.108 \hbox{ cal/g}^o\hbox{C})(65^o\hbox{C}) + (500 \hbox{ g})(1 \hbox{ cal/g}^o\hbox{C})(20^o\hbox{C})} \over {(100 \hbox{ g})(0.108 \hbox{ cal/g}^o\hbox{C}) + (500 \hbox{ g})(1 \hbox{ cal/g}^o\hbox{C})}}\]
\[T = 20.95 \> ^o\hbox{C}\]
Thus, the iron’s temperature falls from 65 degrees Celsius to 20.95 degrees Celsius, while the water’s temperature rises from 20 degrees Celsius to 20.95 degrees Celsius. The water’s tremendous specific heat value compared to the iron (nearly 10 times as much!), as well as its superior mass (5 times as much) results in a much larger temperature change for the iron than for the water.
An analogy to help grasp the concept of specific heat is to imagine heat as a fluid that may be “poured” into vessels of different size, those vessels being objects or substances to be heated. The amount of liquid held by any vessel represents the total amount of thermal energy, while the height of the liquid inside any vessel represents its temperature:

The factor determining the relationship between liquid volume (heat) and liquid height (temperature) is of course the cross-sectional area of the vessel. The wider the vessel, the more heat will be required to “fill” it up to any given temperature. In this analogy, the area of the vessel is analogous to the term \(mc\): the product of mass and specific heat. Objects with larger mass require more heat to raise their temperature to any specific point, specific heats being equal. Likewise, objects with large specific heat values require more heat to raise their temperature to any specific point, masses being equal.
In the first numerical calculation example where we determined the temperature of a pot of water after 40 seconds of heating, the analogous model would be to determine the height of liquid in a vessel after pouring liquid into it for 40 seconds at a fixed rate. A model for the second numerical example would be to calculate the equilibrium height (of liquid) after connecting two vessels together at their bottoms with a tube. Although the liquid heights of those vessels may be different at first, the levels will equalize after time by way of liquid passing through the tube from the higher-level vessel to the lower-level vessel.
Many industrial processes use fluids to convectively transfer thermal energy from one object (or fluid) to another. In such applications, it is important to know how much thermal energy will be carried by a specific quantity of that fluid over a specified temperature drop. One common way to express this quantity is called enthalpy. Enthalpy is the amount of heat lost by a unit mass (one gram metric, or one pound British) of a substance as it cools from a given temperature all the way down to the freezing point of water (0 degrees Celsius, or 32 degrees Fahrenheit). In other words, enthalpy is a measure of a substance’s thermal energy using the freezing temperature of water as a reference. A sample of water at a temperature of 125 degrees Fahrenheit, for example, has an enthalpy of 93 BTU per pound (or 93 calories per gram), because 93 BTU of thermal energy would be lost if one pound of that water happened to cool from its given temperature (125 \(^{o}\)F) down to 32 \(^{o}\)F:
\[Q = mc \Delta T\]
\[Q = (1 \hbox{ lb})\left(1 {\hbox{BTU} \over {\hbox{lb}^o\hbox{F}}}\right)(125 \> ^o\hbox{F} - 32 \> ^o\hbox{F})\]
\[Q = 93 \hbox{ BTU}\]
Even if the substance in question does not cool down to the freezing temperature of water, enthalpy is a useful figure for comparing the thermal energy “content” of hot fluids (per unit mass). For example, if one were given the enthalpy values for a substance before and after heat transfer, it would be easy to calculate the amount of heat transfer that transpired simply by subtracting those enthalpy values. If water at 125 \(^{o}\)F has an enthalpy value of 93 BTU/lb and water at 170 \(^{o}\)F has an enthalpy of value 138 BTU/lb, we may calculate the amount of heat needed to increase the temperature of a sample of water from 125 \(^{o}\)F to 170 \(^{o}\)F simply by subtracting 93 BTU/lb from 138 BTU/lb to arrive at 45 BTU/lb.
In this rather trivial example, it would have been just as easy for us to calculate the heat necessary to increase water’s temperature from 125 \(^{o}\)F to 170 \(^{o}\)F by using the specific heat formula (\(Q = mc \Delta T\)), and so it might appear as though the concept of enthalpy sheds no new light on the subject of heat transfer. However, the ability to calculate heat transfer based on a simple subtraction of enthalpy values proves quite useful in more complex scenarios where substances change phase, as we will see next.
Scientists often speak of four phases of matter: solid, liquid, gas (or vapor), and plasma. Of these four, the first three are common to everyday life. Plasma is a phase of matter where the atoms of a gas are excited (energized) to the point where they become electrically ionized, such as neon gas in an electric tube light, or the gas comprising stars in space.
Phase changes are very important in thermodynamics, principally because energy transfer (heat loss or heat gain) must occur for a substance to change states, often with negligible change in temperature. To cite an example, consider the case of water (a liquid) turning into steam (a vapor) at atmospheric pressure. At sea level, this phase change will occur at a temperature of 100 degrees Celsius, or 212 degrees Fahrenheit. The amount of energy required to increase the temperature of water from ambient up to its boiling point is a simple function of the sample’s mass and its original temperature. For instance, a sample of water 70 grams in mass starting at 24 degrees Celsius will require 5320 calories of heat to reach the boiling point:
\[Q = mc \Delta T\]
\[Q = (70 \hbox{ g})\left(1 {\hbox{cal} \over {\hbox{g}^o\hbox{C}}}\right)(100 \> ^o\hbox{C} - 24 \> ^o\hbox{C})\]
\[Q = 5320 \hbox{ cal}\]
However, actually boiling the 70 grams of water into 70 grams of steam (both at 100 degrees Celsius) requires a comparatively enormous input of heat: 37734 calories – over seven times as much heat to turn the water to steam as what is required to warm the water to its boiling point! Furthermore, this additional input of 37734 calories does not increase the temperature of the water at all: the resulting steam is still at a temperature of (only) 100 degrees Celsius. If further heat is added to the 70 gram steam sample, its temperature will rise, albeit at a rate proportional to the value of steam’s specific heat (0.476 calories per gram degree Celsius, or BTU per pound degree Fahrenheit).
What we see here is a fundamentally different phenomenon than we saw with specific heat. Here, we are looking at the thermal energy required to transition a substance from one phase to another, not to change its temperature. We call this quantity latent heat rather than specific heat, because no temperature change occurs. Conversely, if we allow the steam to condense back into liquid water, it must release the same 37734 calories of heat energy we invested in it turning the water into steam before it may cool at all below the boiling point (100 degrees Celsius).
Latent heat has the effect of greatly increasing a substance’s enthalpy. Recall that “enthalpy” is the amount of heat lost by one pound (mass) of a substance if it happened to cool from its given temperature all the way down to the freezing temperature of water (0 \(^{o}\)C, or 32 \(^{o}\)F). Hot water has an enthalpy of 1 BTU/lb for every degree of temperature above freezing. Steam, however, possesses far greater enthalpy because of the latent heat released in the phase change from vapor to liquid before it releases heat as water cooling down to 32 \(^{o}\)F.
As with specific heat, there is a formula relating mass, latent heat, and heat exchange:
\[Q = mL\]
Where,
\(Q\) = Heat of transition required to completely change the phase of a sample (metric calories or British BTU)
\(m\) = Mass of sample (metric grams or British pounds)
\(L\) = Latent heat of substance
Each substance has its own set of latent heat values, one for each phase-to-phase transition. Water, for example, exhibits a latent heat of vaporization (boiling/condensing) of 539.1 calories per gram, or 970.3 BTU per pound, at atmospheric pressure (boiling point = 100 \(^{o}\)C = 212 \(^{o}\)F). Water also exhibits a latent heat of fusion (melting/freezing) of 79.7 calories per gram, or 143.5 BTU per pound. Both figures are enormous compared to water’s specific heat value of 1 calorie per gram-degree Celsius (or 1 BTU per pound-degree Fahrenheit): it takes only one calorie of heat to warm one gram of water one degree Celsius, but it takes 539.1 calories of heat to boil that same gram of water into one gram of steam, and 79.7 calories of heat to melt one gram of ice into one gram of water. The lesson here is simple: phase changes involve huge amounts of heat.
A table showing various latent heats of vaporization (all at room temperature, 70 degrees Fahrenheit) for common industrial fluids appears here, contrasted against their specific heat values (as liquids). In each case you will note how much larger \(L\) is than \(c\):
| Fluid (@ 70 $^{o}$F) | $L_{vaporization}$, BTU/lb | $L_{vaporization}$, cal/g & $c_{liquid}$ | |
|---|---|---|---|
| Water | 970.3 | 539.1 | 1 |
| Ammonia | 508.6 | 282.6 | 1.1 |
| Carbon dioxide | 63.7 | 35.4 | 0.66 |
| Butane | 157.5 | 87.5 | 0.56 |
| Propane | 149.5 | 83.06 | 0.6 |
One of the most important, and also non-intuitive, consequences of latent heat is the relative stability of temperature during the phase-change process. Referencing the table of latent heats of vaporization, we see how much more heat is needed to boil a liquid into a vapor than is needed to warm that same liquid by one degree of temperature. During the process of boiling, all heat input to the liquid goes into the task of phase change (latent heat) and none of it goes into increased temperature. In fact, until all the liquid has been vaporized, the liquid’s temperature cannot rise above its boiling point! The requirement of heat input to vaporize a liquid forces temperature to stabilize (not rise further) until all the liquid has evaporated from the sample.
If we take a sample of ice and add heat to it over time until it melts, warms, boils, and then becomes steam, we will notice a temperature profile that looks something like this:
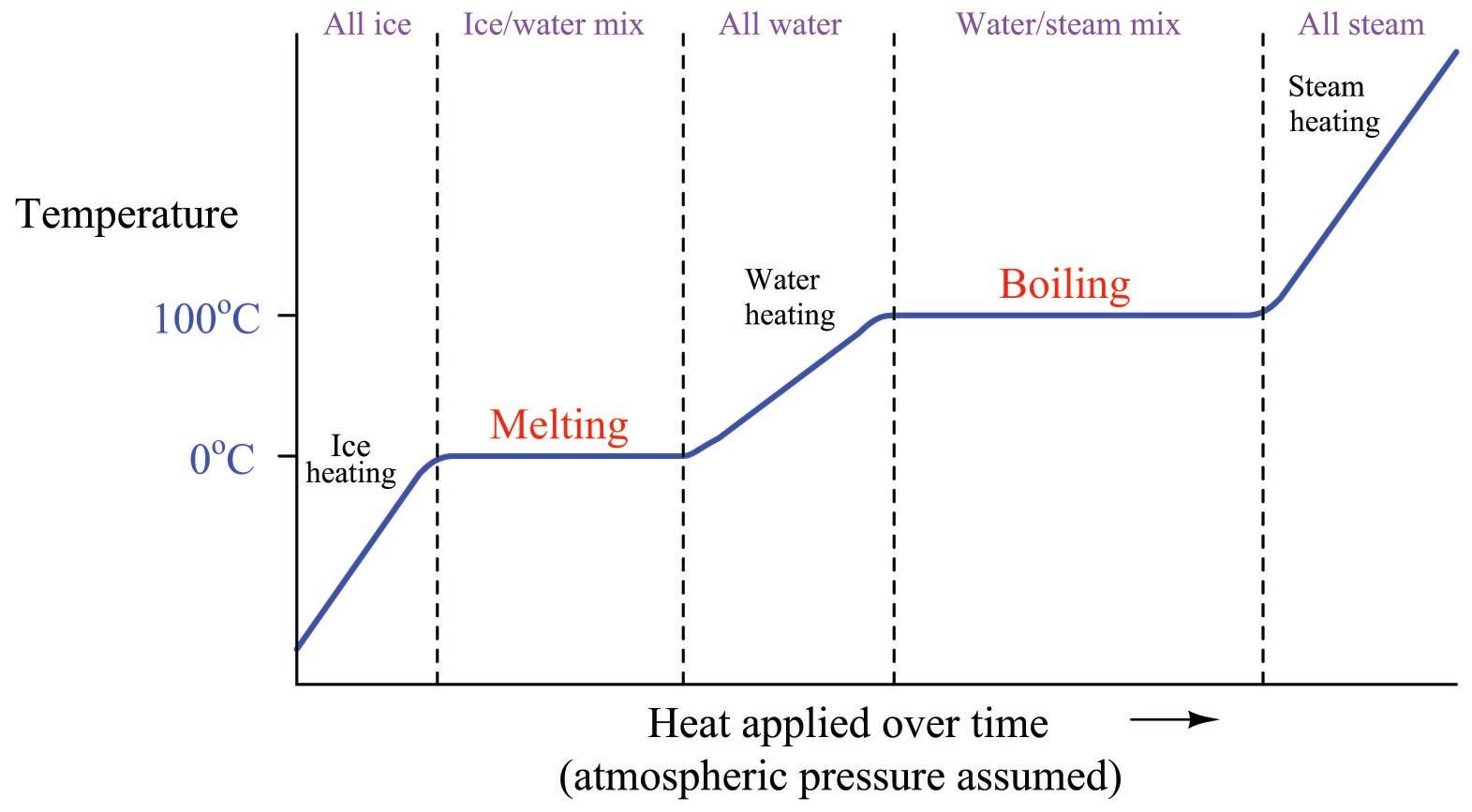
The flat areas of the graph during the melting and boiling periods represents times where the sample’s temperature does not change at all, but where all heat input goes into the work of changing the sample’s phase. Only where we see the curve rising does the temperature change. So long as there is a mixture of different phases, the temperature remains “locked” at one value. Only when there is a single phase of material is the temperature “allowed” to rise or fall.
The sloped areas of the graph reveal the specific heat of the substance in each particular phase. Note how the liquid (water) portion of the graph has a relatively shallow slope, due to the specific heat value (\(c\)) of water being equal to 1. Both the ice and the steam portions of the graph have steeper slopes because both of those phases possess smaller values of specific heat (\(c = 0.5\) and \(c = 0.476\), respectively). The smaller the value of \(c\), the more a sample’s temperature will rise for any given input of thermal energy. For any given rate of heat transfer, smaller \(c\) values result in more rapid temperature changes.
We may employ our liquid-filled vessel analogy to the task of explaining latent heat. Any point of phase change is analogous to a point along the vessel’s height equipped with a large expansion chamber, so that the vessel “acts” as if its area were much larger at one point, requiring much more fluid volume (heat) to change height (temperature) past that one point:

Liquid poured into this vessel will fill it at a rate proportional to the volume added and inversely proportional to the vessel’s cross-sectional area at the current liquid height. As soon as the liquid level reaches the expansion chamber, a great deal more liquid must be added to cause level to increase, since this chamber must completely fill before the liquid level may rise above it. Once that happens, the liquid level rises at a different rate with addition introduced volume, because now the phase is different (with a different specific heat value).
Remember that the filling of a vessel with liquid is merely an analogy for heat and temperature, intended to provide an easily visualized process mimicking another process not so easily visualized. The important concept to realize with latent heat and phase change is that it constitutes a discontinuity in the temperature/heat function for any given substance.
A vivid demonstration of this phenomenon is to take a paper cup filled with water and place it in the middle of a roaring fire. “Common sense” might tell you the paper will burn through with the fire’s heat, so that the water runs out of the cup through the burn-hole. This does not happen, however. Instead, the water in the cup will rise in temperature until it boils, and there it will maintain that temperature no matter how hot the fire burns. The boiling point of water happens to be substantially below the burning point of paper, and so the boiling water keeps the paper cup too cool to burn. As a result, the paper cup remains intact so long as water remains in the cup. The rim of the cup above the water line will burn up because the steam does not have the same temperature-stabilizing effect as the water, leaving a rimless cup that grows shorter as the water boils away.
The point at which a pure substances changes phase not only relates to temperature, but to pressure as well. We may speak casually about the boiling point of water being 100 degrees Celsius (212 degrees Fahrenheit), but that is only if we assume the water and steam are at atmospheric pressure (at sea level). If we reduce the ambient air pressure, water will boil at a lesser temperature. Anyone familiar with cooking at high altitudes knows you must generally cook for longer periods of time at altitude, because the decreased boiling temperature of water is not as effective for cooking. Conversely, anyone familiar with pressure cooking (where the cooking takes place inside a vessel pressurized by steam) knows how comparatively little cooking time is required because the pressure raises water’s boiling temperature. In either of these scenarios, where pressure influences boiling temperature, the latent heat of water acts to hold the boiling water’s temperature stable until all the water has boiled away. The only difference is the temperature at which the water begins to boil (or when the steam begins to condense).
Many industrial processes use boiling liquids to convectively transfer heat from one object (or fluid) to another. In such applications, it is important to know how much heat will be carried by a specific quantity of the vapor as it condenses into liquid over a specified temperature drop. The quantity of enthalpy (heat content) used for rating the heat-carrying capacity of liquids applies to condensing vapors as well. Enthalpy is the amount of heat lost by a unit mass (one gram metric, or one pound British) of the fluid as it cools from a given temperature all the way down to the freezing point of water (0 degrees Celsius, or 32 degrees Fahrenheit). When the fluid’s initial state is vapor, and it condenses into liquid as it cools down to the reference temperature (32 \(^{o}\)F), the heat content (enthalpy) is not just a function of specific heat, but also of latent heat.
Water at its atmospheric boiling point has an enthalpy of approximately 180 BTU per pound. Steam at atmospheric pressure and 212 \(^{o}\)F, however, has an enthalpy of about 1150 BTU per pound: more than six times as much heat as water at the same temperature. 970 of that 1150 BTU/lb is due to the phase change from steam to water, while the rest is due to water’s specific heat as it cools from 212 \(^{o}\)F to 32 \(^{o}\)F.
Many technical reference books contain a set of data known as a steam table showing various properties of steam at different temperatures and pressures. Enthalpy is one of the most important parameters given in a steam table, showing how much available energy resides in steam under different pressure and temperature conditions. For this reason, enthalpy is sometimes referred to as total heat (\(h_g\)). Steam tables also show saturation temperature (the condensing temperature for steam at that pressure) and steam density.
If the vapor in question is at a temperature greater than its boiling point at that pressure, the vapor is said to be superheated. The enthalpy of superheated vapor comes from three different heat-loss mechanisms:
Using steam as the example once more, a sample of superheated steam at 500 \(^{o}\)F and atmospheric pressure (boiling point = 212 \(^{o}\)F) has an enthalpy of approximately 1287 BTU per pound. We may calculate the heat lost by one pound of this superheated steam as it cools from 500 \(^{o}\)F to 32 \(^{o}\)F in each of the three steps previously described. Here, we will assume a specific heat for steam of 0.476, a specific heat for water of 1, and a latent heat of vaporization for water of 970:
| Heat loss mechanism | Formula | Quantity |
|---|---|---|
| Cooling vapor | $Q = mc \Delta T$ | (1)(0.476)($500-212$) = 137 BTU |
| Phase change | $Q = mL$ | (1)(970) = 970 BTU |
| Cooling liquid | $Q = mc \Delta T$ | (1)(1)($212-32$) = 180 BTU |
| TOTAL | 1287 BTU |
Enthalpy values are very useful in steam engineering to predict the amount of thermal energy delivered to a load given the steam’s initial temperature, its final (cooled) temperature, and the mass flow rate. Although the definition of enthalpy – where we calculate heat value by supposing the vapor cools all the way down to the freezing point of water – might seem a bit strange and impractical (how common is it for steam to lose so much heat to a process that it reaches freezing temperature?), it is not difficult to shift the enthalpy value to reflect a more practical final temperature. Since we know the specific heat of liquid water is very nearly one, all we have to do is offset the enthalpy value by the amount that the final temperature differs from freezing in order to calculate how much heat the steam will lose (per pound) to its load.
Furthermore, the rate at which heat is delivered to a substance by steam (or conversely, the rate at which heat is required to boil water into steam) may be easily calculated if we take this heat value in units of BTU per pound and multiply it by the mass flow rate in pounds per minute: as the unit of “pound” cancels in the multiplication, we arrive at a result for heat transfer rate in units of BTU per minute.
For example, suppose we were to employ the same 500 \(^{o}\)F superheated steam used in the previous example to heat a flow of oil through a heat exchanger, with the steam condensing to water and then cooling down to 170 degrees Fahrenheit as it delivers heat to the flowing oil. Here, the steam’s enthalpy value of 1287 BTU per pound may simply be offset by 138 (170 degrees minus 32 degrees) to calculate how much heat (per pound) this steam will deliver to the oil: 1287 \(-\) 138 = 1149 BTU per pound:

Here we see how 500 \(^{o}\)F steam has an enthalpy (total heat) of 1287 BTU/lb, but since the steam does not in fact cool all the way down to 32 \(^{o}\)F in the act of heating oil in the heat exchanger, we must subtract the enthalpy of the 170 \(^{o}\)F water (138 BTU/lb) to determine the amount of heat actually delivered to the oil by the steam (1149 BTU/lb). Calculating heat transfer rate is a simple matter of multiplying this heat per pound of steam by the steam’s mass flow rate: for example, if the mass flow rate of this steam happened to be 2 pounds per minute, the heat transfer rate would be 2298 BTU per minute.
If we happen to be dealing with a situation where steam gives up some heat energy to a process fluid but not enough to cool to the point of condensation, all we need to do to calculate the amount of heat liberated by the superheated steam as it cools is subtract the enthalpy values between its hot and cool(er) states.
For example, suppose we have a heat-exchange process where superheated steam enters at 105 PSIG and 600 \(^{o}\)F, exiting at 75 PSIG and 360 \(^{o}\)F. The enthalpy of the steam under those two sets of conditions as given by a superheated steam table are 1328 BTU/lb and 1208 BTU/lb, respectively. Thus, the heat lost by the steam as it goes through this heat exchanger is the difference in enthalpy values: 1328 BTU/lb \(-\) 1208 BTU/lb = 120 BTU/lb. Once again, calculating heat transfer rate is a simple matter of multiplication: if the mass flow rate of this steam happened to be 80 pounds per hour, the heat transfer rate would be 120 BTU/lb \(\times\) 80 lb/hr = 9600 BTU/hr.
By encompassing both specific heat and latent heat into one quantity, enthalpy figures given in steam tables greatly simplify heat transfer calculations, as compared to evaluating specific heat and latent heat formulae (\(Q = mc \Delta T\) and \(Q = mL\), respectively) for water. Calculations based on steam tables are also more accurate than those derived from the specific and/or latent heat formulae, because steam tables take into account the changing values of \(c\) and \(L\) over wide temperature and pressure ranges. This is the power of empirical data: steam tables were developed by taking actual calorimetric measurements of steam under those temperature and pressure conditions, and as such are a record of water’s true behavior rather than a prediction of water’s theoretical behavior.
A comprehensive way of describing the relationship between pressure, temperature, and substance phase is with something called a phase diagram. With pressure shown on one axis, and temperature on the other, a phase diagram describes the various phases of a substance in possible equilibrium at certain pressure/temperature combinations.

This phase diagram (for water) illustrates some of the features common to all phase diagrams: curved lines define the boundaries between solid, liquid, and vapor phases; the point of intersection of these three curves is where the substance may exist in all three phases simultaneously (called the triple point) and points where a curve simply ends within the span of the graph indicate critical points, where the certain phases cease to exist.
The curved line from the triple point up and to the right defines the boundary between liquid water and water vapor. Each point on that line represents a set of unique pressure and temperature conditions for boiling (changing phase from liquid to vapor) or for condensation (changing phase from vapor to liquid). As you can see, increased pressure results in an increased boiling point (i.e. at higher pressures, water must be heated to greater temperatures before boiling may take place). In fact, the whole concept of a singular boiling point for water becomes quaint in the light of a phase diagram: boiling is seen to occur over a wide range of temperatures, the exact temperature varying with pressure.
Something interesting happens when the temperature is raised above a certain value called the critical temperature. At this value (approximately 374 degrees Celsius for water), no amount of pressure will maintain it in a liquid state. Water, once heated beyond 374 degrees Celsius, is no longer a liquid and may only exist in a stable condition as a vapor. The critical pressure of any substance is the pressure value at the liquid/vapor boundary at the point of critical temperature.
A vivid example of critical temperature is this photograph of an ultra-high pressure storage vessel for oxygen gas, at a rocket engine testing facility:

The critical temperature for oxygen is 154.58 Kelvin, which is equal to \(-118.57\) degrees Celsius or \(-181.43\) degrees Fahrenheit. Since this pressure vessel is completely uninsulated, we know the temperature of the oxygen inside of it will be the same (or nearly the same) as ambient temperature, which is obviously much warmer than \(-118.57\) \(^{o}\)C. Since the oxygen’s temperature is well above the critical temperature for the element oxygen, we may safely conclude that the oxygen inside this vessel must exist as a gas. Even at the extremely high pressure this vessel is capable of holding (15000 PSIG), the oxygen cannot liquefy.
The slightly curved line from the triple point up and to the left defines the boundary between solid ice and liquid water. As you can see, the near-vertical pitch of this curve suggests the freezing temperature of water is quite stable over a wide pressure range.
Carbon dioxide exhibits a different set of curves than water on its phase diagram, with its own unique critical temperature and pressure values:

Note how the triple-point pressure of carbon dioxide is well above ambient conditions on Earth. This means carbon dioxide is not stable in its liquid state unless put under substantial pressure (at least 60.4 PSIG). This is why solid carbon dioxide is referred to as dry ice: it does not liquefy with the application of heat, rather it sublimates directly into its vapor phase.
Another interesting difference between the carbon dioxide and water phase diagrams is the slope of the solid/liquid boundary line. With water, this boundary drifts to the left (lower temperature) as pressure increases. With carbon dioxide, this boundary drifts to the right (higher temperature) as pressure increases. Whether the fusion temperature increases or decreases with increasing pressure marks whether that substance contracts or expands as it transitions from liquid to solid. Carbon dioxide, like most pure substances, contracts to a smaller volume when it goes from liquid to solid, and its fusion curve drifts to the right as pressure increases. Water is unusual in this regard, expanding to a larger volume when freezing, and its fusion curve drifts to the left as pressure increases.
A saturated steam table shows temperatures and pressures for water at the liquid/vapor transition (i.e. points lying along the liquid/vapor interface shown in a phase change diagram), as well as enthalpy values for the water and steam under those conditions. The sensible heat of water is the amount of thermal energy per pound necessary to raise water’s temperature from the freezing point to the boiling point. The latent heat of vapor is the amount of energy per pound necessary to convert water (liquid) into steam (vapor). The total heat is the enthalpy of steam (thermal energy per pound) between the listed condition in the table and the freezing temperature of water.
By definition a saturated steam table does not describe steam at temperatures greater than the boiling point. For such purposes, a superheated steam table is necessary.
Data for this saturated steam table was taken from Thermal Properties of Saturated and Superheated Steam by Lionel Marks and Harvey Davis, published in 1920 by Longmans, Green, and Company.
Saturated Steam Table
| Temperature | Pressure | Sensible heat of | Latent heat of | Total heat |
| (Deg F) | (PSIA) | liquid (BTU/lb) | vapor (BTU/lb) | (BTU/lb) |
| 32 | 0.0886 | 0.00 | 1073.4 | 1073.4 |
| 40 | 0.1217 | 8.05 | 1068.9 | 1076.9 |
| 50 | 0.1780 | 18.08 | 1063.3 | 1081.4 |
| 60 | 0.2562 | 28.08 | 1057.8 | 1085.9 |
| 70 | 0.3626 | 38.06 | 1052.3 | 1090.3 |
| 80 | 0.505 | 48.03 | 1046.7 | 1094.8 |
| 50 | 0.696 | 58.00 | 1041.2 | 1099.2 |
| 60 | 0.2562 | 28.08 | 1057.8 | 1085.9 |
| 70 | 0.3626 | 38.06 | 1052.3 | 1090.3 |
| 80 | 0.505 | 48.03 | 1046.7 | 1094.8 |
| 90 | 0.696 | 58.00 | 1041.2 | 1099.2 |
| 100 | 0.946 | 67.97 | 1035.6 | 1103.6 |
| 110 | 1.271 | 77.94 | 1030.0 | 1108.0 |
| 120 | 1.689 | 87.91 | 1024.4 | 1112.3 |
| 130 | 2.219 | 97.89 | 1018.8 | 1116.7 |
| 140 | 2.885 | 107.87 | 1013.1 | 1121.0 |
| 150 | 3.714 | 117.86 | 1007.4 | 1125.3 |
| 160 | 4.737 | 127.86 | 1001.6 | 1129.5 |
| 170 | 5.992 | 137.87 | 995.8 | 1133.7 |
| 180 | 7.51 | 147.88 | 989.9 | 1137.8 |
| 190 | 9.34 | 157.91 | 983.9 | 1141.8 |
| 200 | 11.52 | 167.94 | 977.8 | 1145.8 |
| 210 | 14.13 | 177.99 | 971.6 | 1149.6 |
| 212 | 14.70 | 180.00 | 970.4 | 1150.4 |
Saturated Steam Table (continued)
| Temperature | Pressure | Sensible heat of | Latent heat of | Total heat |
| (Deg F) | (PSIA) | liquid (BTU/lb) | vapor (BTU/lb) | (BTU/lb) |
| 220 | 17.19 | 188.1 | 965.2 | 1153.3 |
| 230 | 20.77 | 198.2 | 958.7 | 1156.9 |
| 240 | 24.97 | 208.3 | 952.1 | 1160.4 |
| 250 | 29.82 | 218.5 | 945.3 | 1163.8 |
| 260 | 35.42 | 228.6 | 938.4 | 1167.0 |
| 270 | 41.85 | 238.8 | 931.4 | 1170.2 |
| 280 | 49.18 | 249.0 | 924.3 | 1173.3 |
| 290 | 57.55 | 259.3 | 916.9 | 1176.2 |
| 300 | 67.00 | 269.6 | 909.5 | 1179.1 |
| 310 | 77.67 | 279.9 | 901.9 | 1181.8 |
| 320 | 89.63 | 290.2 | 894.2 | 1184.4 |
| 330 | 103.0 | 300.6 | 886.3 | 1186.9 |
| 340 | 118.0 | 311.0 | 878.3 | 1189.3 |
| 350 | 134.6 | 321.4 | 870.1 | 1191.5 |
| 360 | 153.0 | 331.9 | 861.8 | 1193.7 |
| 370 | 173.3 | 342.4 | 853.4 | 1195.8 |
| 380 | 195.6 | 352.9 | 844.8 | 1197.7 |
| 390 | 220.2 | 363.5 | 836.1 | 1199.6 |
| 400 | 247.1 | 374.1 | 827.2 | 1201.3 |
| 410 | 276.4 | 384.7 | 818.2 | 1202.9 |
| 420 | 308.4 | 395.4 | 809.0 | 1204.4 |
| 430 | 343.2 | 406.2 | 799.6 | 1205.8 |
| 440 | 380.8 | 417.0 | 790.1 | 1207.1 |
If we look at the areas bounded by phase transition curves in a phase diagram (solid area, liquid area, and vapor area), we see that both pressure and temperature may change independent of one another. A vessel filled with liquid water, for instance, may be at 30 degrees Celsius and 2 atmospheres, or at 50 degrees Celsius and 2 atmospheres, or at 50 degrees Celsius and 1 atmosphere, all equally stable. A more technical way to state this is to say the liquid water has two degrees of freedom. Here, the word “degree” has a completely different meaning than it does when used to denote a unit of temperature or angle. In this context, “degree” may be thought of loosely as “dimension.” A cube has three physical dimensions, a square has two and a line has one. A point within a cube has three degrees of freedom (motion), while a point within a square only has two, and a point along a line only has one. Here, we use the word “degree” to denote the number of independent ways a system may change. For areas bounded by phase transition curves in a phase diagram, pressure and temperature are the two “free” variables, because within those bounded areas we may freely alter pressure without altering temperature, and vice-versa.
Such is not the case at any point lying along one of the phase transition curves. Any point on a curve is geometrically defined by a pair of coordinates, which means that for a two-phase mixture in equilibrium there will be exactly one temperature value valid for each unique pressure value. At any point along a phase transition curve, pressure and temperature are not independent variable, but rather are related. This means that for any single substance, there is only one degree of freedom along any point of a phase transition curve.
To illustrate this concept, suppose we equip a closed vessel containing water with both a thermometer and a pressure gauge. The thermometer measures the temperature of this water, while the pressure gauge measures the pressure of the water. A burner beneath the vessel adds heat to alter the water’s temperature, and a pump adds water to the vessel to alter the pressure inside:

So long as the water is all liquid (one phase), we may adjust its pressure and temperature independently. In this state, the system has two thermodynamic degrees of freedom.
However, if the water becomes hot enough to boil, creating a system of two phases in direct contact with each other (equilibrium), we will find that pressure and temperature become linked: one cannot alter one without altering the other. For a steam boiler, operation at a given steam pressure thus defines the temperature of the water, and vice-versa. In a single-component, two-phase system, there is only one degree of thermodynamic freedom.
Our freedom to alter pressure and temperature becomes even more restricted if we ever reach the triple point of the substance. For water, this occurs (only) at a pressure of \(-14.61\) PSIG (0.006 atmospheres) and a temperature of 0.01 degrees Celsius: the coordinates where all three phase transition curves intersect on the phase diagram. In this state, where solid (ice), liquid (water), and vapor (steam) coexist, there are zero degrees of thermodynamic freedom. Both the temperature and pressure are locked at these values until one or more of the phases disappears.
The relationship between degrees of freedom and phases is expressed neatly by Gibbs’ Phase Rule – the sum of phases and degrees of freedom equals the number of substances (“components”) plus two:
\[N_{freedom} + N_{phase} = N_{substance} + 2\]
We may simplify Gibbs’ rule for systems of just one substance (1 “component”) by saying the number of degrees of freedom plus phases in direct contact with each other is always equal to three. So, a vessel filled with nothing but liquid water (one component, one phase) will have two thermodynamic degrees of freedom: we may change pressure or temperature independently of one another. A vessel containing nothing but boiling water (two phases – water and steam, but still only one component) has just one thermodynamic degree of freedom: we may change pressure and temperature, but just not independently of one another. A vessel containing water at its triple point (three phases, one component) has no thermodynamic freedom at all: both temperature and pressure are fixed so long as all three phases coexist in equilibrium.
Applications of phase changes abound in industrial and commercial processes. Some of these applications exploit phase changes for certain production goals, such as the storage and transport of energy. Others merely serve to illustrate certain phenomena such as latent heat and degrees of thermodynamic freedom. This subsection will highlight several different processes for your learning benefit.
A common example of a saturated liquid/vapor (two-phase) system is the internal environment of a propane storage tank, such as the kind commonly used to store propane fuel for portable stoves and gas cooking grills. If multiple propane storage tanks holding different volumes of liquid propane are set side by side, pressure gauges attached to each tank will all register the exact same pressure:

This is counter-intuitive, as most people tend to think the fullest tank should register the highest pressure (having the least space for the vapor to occupy). However, since the interior of each tank is a liquid/vapor system in equilibrium, the pressure is defined by the point on the liquid/vapor transition curve on the phase diagram for pure propane matching the tanks’ temperature. Thus, the pressure gauge on each tank actually functions as a thermometer, since pressure is a direct function of temperature for a saturated liquid/vapor system and therefore cannot change without a corresponding change in temperature. This is a thermodynamic system with just one degree of freedom.
Storage tanks containing liquid/vapor mixtures in equilibrium present unique safety hazards. If ever a rupture were to occur in such a vessel, the resulting decrease in pressure causes the liquid to spontaneously boil, halting any further decrease in pressure. Thus, a punctured propane tank does not lose pressure in the same manner than a punctured compressed air tank loses pressure. This gives the escaping vapor more “power” to worsen the rupture, as its pressure does not fall off over time the way it would in a simple compressed-gas application. As a result, relatively small punctures can and often do grow into catastrophic ruptures, where all liquid previously held inside the tank escapes and flashes into vapor, generating a vapor cloud of surprisingly large volume.
Compounding the problem of catastrophic tank rupture is the fact that propane happens to be highly flammable. The thermodynamic properties of a boiling liquid combined with the chemical property of flammability in air makes propane tank explosions particularly violent. Fire fighters often refer to this as a BLEVE: a Boiling Liquid Expanding Vapor Explosion.
This same pressure-temperature interdependence finds application in a type of temperature measurement instrument called a Class II filled-bulb, where a metal bulb, tube, and pressure-sensing element are all filled with a saturated liquid/vapor mixture:

Heat applied to the bulb literally “boils” the liquid inside until its pressure reaches the equilibrium point with temperature. As the bulb’s temperature increases, so does the pressure throughout the sealed system, indicating at the operator display where a bellows (or some other pressure-sensing element) moves a pointer across a calibrated scale.
The only difference between the two filled-bulb thermometers shown in the illustration is which end of the instrument is warmer. The Class IIA system on the left (where liquid fills the pressure-indicating element) is warmer at the bulb than at the indicating end. The Class IIB system on the right (where vapor fills the indicating bellows) has a cooler bulb than the indicating bellows. The long length and small internal diameter of the connecting tube prevents any substantial heat transfer from one end of the system to the other, allowing the sensing bulb to easily be at a different temperature than the indicating bellows. Both types of Class II thermometers work the same, the indicated pressure being a strict function of the bulb’s temperature where the liquid and vapor coexist in equilibrium.
Nuclear reactors using pressurized water as the moderating and heat-transfer medium must maintain the water coolant in liquid form despite the immense heat output of the reactor core, to avoid the formation of steam bubbles within the reactor core which could lead to destructive “hot spots” inside the reactor. The following diagram shows a simplified pressurized water reactor (PWR) cooling system:

In order to maintain a liquid-only cooling environment for the reactor core, the water is held at a pressure too high for boiling to occur inside the reactor vessel. Typical operating conditions for a pressurized water reactor are 575 \(^{o}\)F and 2100 PSIG. A steam table shows the boiling point of water at 2100 PSIG to be over 640 \(^{o}\)F, which means the water inside the reactor cannot boil if the reactor only operates at 575 \(^{o}\)F. Referencing the phase diagram for water, the operating point of the reactor core is maintained above the liquid/vapor phase transition line by an externally supplied pressure.
This excess pressure comes from a device in the primary coolant loop called a pressurizer. Inside the pressurizer is an array of immersion-style electric heater elements. The pressurizer is essentially an electric boiler, purposely boiling the water inside at a temperature greater than that reached by the reactor core itself. For the example figure of 2100 PSIG, the pressurizer elements would have to operate at a temperature of approximately 644 \(^{o}\)F to maintain a boiling condition inside the pressurizer.
By maintaining the water temperature inside the pressurizer greater than at the reactor core, the water flowing through the reactor core literally cannot boil. The water/vapor equilibrium inside the pressurizer is a system with one degree of freedom (pressure and temperature linked), while the water-only environment inside the reactor core has two degrees of freedom (temperature may vary to any amount below the pressurizer’s temperature without water pressure changing at all). Thus, the pressurizer functions like the temperature-sensing bulb of a gigantic Class IIA filled-bulb thermometer, with a liquid/vapor equilibrium inside the pressurizer vessel and liquid only inside the reactor vessel and all other portions of the primary coolant loop. Reactor pressure is then controlled by the temperature inside the pressurizer, which is in turn controlled by the amount of power applied to the heating element array.
Boilers in general (the nuclear reactor system previously described being just one example of a large “power” boiler) are outstanding examples of phase change applied to practical use. The purpose of a boiler is to convert water into steam, sometimes for heating purposes, sometimes as a means of producing mechanical power (through a steam engine), sometimes for chemical processes requiring pressurized steam as a reactant, sometimes for utility purposes (maintenance-related cleaning, process vessel purging, sanitary disinfection, fire suppression, etc.) or all of the above. Steam is a tremendously useful substance in many industries, so you will find boilers in use at almost every industrial facility.
A simplified diagram of a water tube boiler appears here:

Water enters the boiler through a heat exchanger in the stack called an economizer. This allows cold water to be pre-heated by the warm exhaust gases before they exit the stack. After pre-heating in the economizer, the water enters the boiler itself, where water circulates by natural convection (“thermosiphon”) through a set of tubes exposed to high-temperature fire. Steam collects in the “steam drum,” where it is drawn off through a pipe at the top. Since this steam is in direct contact with the boiling water, it will be at the same temperature as the water, and the steam/water environment inside the steam drum represents a two-phase system with only one degree of freedom. With just a single degree of freedom, steam temperature and pressure are direct functions of each other – coordinates at a single point along the liquid/vapor phase transition line of water’s phase diagram. One cannot change one variable without changing the other.
Consulting a steam table, you will find that the temperature required to boil water at a pressure of 120 PSIG is approximately 350 degrees Fahrenheit. Thus, the temperature of the steam drum will be fixed at 350 \(^{o}\)F while generating steam pressure at 120 PSIG. The only way to increase pressure in that boiler is to increase its temperature, and vice-versa.
When steam is at the same temperature as the boiling water it came from, it is referred to as saturated steam. Steam in this form is very useful for heating and cleaning, but not as much for operating mechanical engines or for process chemistry. If saturated steam loses any temperature at all (by losing its latent heat), it immediately condenses back into water. Liquid water can cause major mechanical problems inside steam engines (although “wet” steam works wonderfully well as a cleaning agent!), and so steam must be made completely “dry” for some process applications.
The way this is done is by a process known as superheating. If steam exiting the steam drum of a boiler is fed through another heat exchanger inside the firebox so it may receive more heat, its temperature will rise beyond the saturation point. This steam is now said to be superheated:
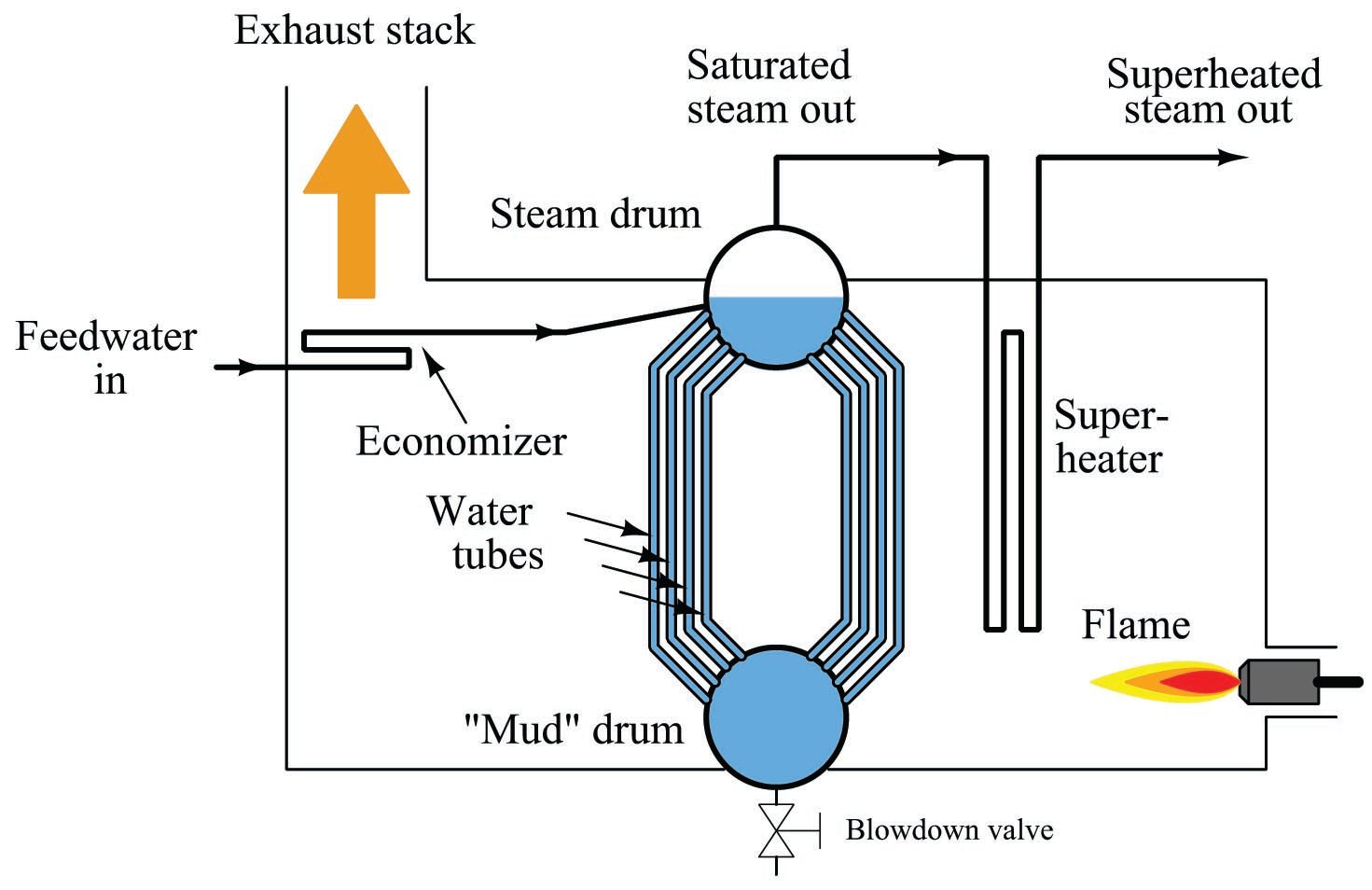
Superheated steam is absolutely dry, containing no liquid water at all. It is therefore safe to use as a fluid medium for engines (piston and turbine alike) and as a process reactant where liquid water is not tolerable. The difference in temperature between superheated steam and saturated steam at any given pressure is the amount of superheat. For example, if saturated steam at 350 degrees Fahrenheit and 120 PSI drawn from the top of the steam drum in a boiler is heated to a higher temperature of 380 degrees Fahrenheit (at the same pressure of 120 PSI), it is said to have 30 degrees (Fahrenheit) of superheat.
An interesting application of phase changes and latent heat occurs in agriculture. Fruit growers, needing to protect their budding crop from the damaging effects of a late frost, will spray water over the fruit trees to maintain the sensitive buds above freezing temperature. As cold air freezes the water, the water’s latent heat of fusion prevents the temperature at the ice/water interface from dropping below 32 degrees Fahrenheit. So long as liquid water continues to spray over the trees, the buds’ temperature cannot fall below freezing. Indeed, the buds cannot even freeze in this condition, because once they cool down to the freezing point, there will be no more temperature difference between the freezing water and the buds. With no difference of temperature, no heat will transfer out of the buds. With no heat loss, water inside the buds cannot change phase from liquid to solid (ice) even if held at the freezing point for long periods of time, thus preventing freeze damage. Only if the buds are exposed to cold air (below the freezing point), or the water turns completely to ice and no longer holds stable at the freezing point, can the buds themselves ever freeze solid.
A very common use of a liquid-to-vapor phase change is for cooling purposes: taking hot water and mechanically forcing that hot water to evaporate in order to remove large quantities of heat energy from the water, thus cooling it to a lower temperature. Devices called evaporative cooling towers accomplish this task by causing ambient air to flow past droplets of water. As the rising air contacts the falling water droplets, some of the water is forced to evaporate, the heat required of this evaporation being provided by sensible heat within the remaining liquid water. As a result, the still-liquid water must cool in temperature as it gives up heat energy to the newly-formed water vapor.

Smaller evaporative cooling towers use fans to force air upward through the tower, employing inert “fill” material to provide large amounts of surface area for the liquid water and the air to contact each other. Some large evaporative cooling towers are self-drafting, the heat of the water providing enough convective force to the air that no fans are needed.
The following photograph shows a pair of induced-draft evaporative cooling towers used at a beer brewery:

This next photograph shows a forced-draft evaporative cooling tower used at a coal-fired electric power plant. Note the large air fans located around the circumference of the cooling tower, blowing cool air into the tower from outside. This fan placement eliminates problems arising from having the fan blades and motor located within the moist air stream:
