Introduction to Binary Coded Decimal (BCD) Numbers in Instrumentation and Control

While computers are thought of as a way to perform complex mathematical calculations, they really only deal with ones and zeroes. This is because all of their calculations are based on whether certain transistors are switched off, called “false” or “logic zero”, or switched on, called “true” or “logic one”. The transistors can only occupy one of two states (true or false). Believe it or not, the “power” button on many electronic devices is simply a one and a zero put together.

 

Figure 1. The power to this Macbook Pro is either on or off, true or false, as represented by the one and zero found on the power button. Image used courtesy of Wikimedia Commons 

 

So then, how do computers perform calculations using only ones and zeroes, while humans must read numbers in our familiar 0-9 digits to be understood? The answer is that all numbers, commands, user inputs, and displays must be converted to binary for the calculation to occur.

$$~$$

Decimal to Binary Conversion

This number conversion is a way to take regular numbers (decimal or base 10 numbers) and make them understood by a computer. In order to fully understand this, one must first evaluate what they know about base 10 decimal numbers from elementary school. Starting at zero and counting up, there are ten unique symbols:  0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, where adding one to each number gets a new symbol. Once 9 is reached, there is no new symbol for 10. Instead, the ones place starts over (0), and we put a 1 in the tens place. 

In this way, there are not only symbols but a weighted order of appearance. For example, 367 does not equal 736, even though all of those same numbers are present. This is because each symbol’s place matters:

\(3 \cdot 100 = 300\)
\(6 \cdot 10 ~~=~~ 60\)
\(7 \cdot 1 ~~~~= ~~~~7\)
-----------------
\(~~~~~~~~~~~~~~~~ 367\)

Binary numbers work the same way, but instead of a full ten symbols, there are only two—0 and 1. When counting up in binary, the sequence goes 0, 1, 10, 11, 110, 111, and so on. Each time there is a need to add to a 1, that place starts over, and a new place value is added. Consider the binary number 1101. In decimal numbers, this would be:

\(1 \cdot 2^3  =   8\)
\(1 \cdot 2^2  =   4\)
\(0 \cdot 2^1  =   0\)
\(1 \cdot 2^0  =   1\)
-----------------
\(~~~~~~~~~~~~13\)
 

 

Each place value in binary is called a “bit” and could be represented by one transistor. Eight transistors strung together would form a “byte”. 

 

Figure 2. Many sensors, like thermocouples of pressure sensors, can be monitored by a local 7-segment display, and some of these require BCD inputs. Image used courtesy of Adobe Stock

 

Instrumentation Complication

Before the days of common network components, like IO-Link or Ethernet, the data between human and machine (think human-machine interface, the HMI) must be a very simple representation of decimal numbers of the human converted into an equivalent value for the computer.

In the binary examples before, long decimal numbers could be converted into their binary equivalents, but without a calculator, it would be very hard to tell what the decimal value is or how many digits it was in size. With digital networks, a long binary number can be sent down a wire in moments and converted to its decimal equivalent at both ends. Before this was commonplace, a more simple conversion form was designed.

 

What Is Binary Coded Decimal (BCD)?

The solution was to designate each digit of a decimal number into its own unique binary number. Using the example in previous sections, we could see that 0000 = 0 and 1001 = 9. Every other decimal number lies between these two digits. So to represent all of our decimal numbers, we would need 4 bits.

In the BCD system, each decimal digit is assigned its own 4-bit binary number. It can be known in an instant the number of digits in the decimal number and much more conveniently convert each digit.

For example, the decimal number 487 would consist of 12 binary numbers, 4x for each digit.

 

0100 = 4

1000 = 8

0111 = 7

 

Therefore, a full, 16-bit BCD equivalent of 487 would be:

 

0000 0100 0100 0111

 

In the following image, the decimal number 487 is shown converted into both a normal binary integer (right path) and a BCD intended for a 7-segment display (left path).

 

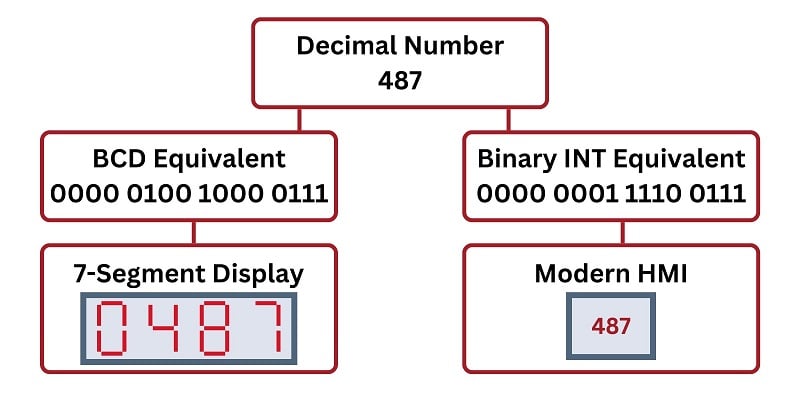
Figure 3. One decimal number can serve two different purposes depending on the binary data type (BCD or INT) to which it is converted.

 

Why Would You Need BCD?

Again, for most modern HMIs and computers, the BCD value is only for interaction with legacy equipment. One of the primary uses of BCD was for 7-segment displays. The integrated circuits that drive the 7-segment LEDs require 4 bits to output a value of 0-9. If your display had six digits, each digit would require its own 4-bit input. This is exactly the purpose of BCD.

When interfacing with older displays and devices, it is possible in many PLCs and control systems to reserve multiples of 4 bits with a BCD data type. The system will recognize how this number converts to decimal and typical binary.

To interface this data with the actual legacy device, multiples of 4x wires for each digit will be required. It is much more bulky and far less efficient than modern single-cable networks, yet it might still be encountered and is worth knowing.

 

Figure 4. Modern PLCs may allow for BCD data types, but it’s not a very common selection these days. Image used courtesy of Adobe Stock

 

BCD Numbers

BCD is not a type of concept in modern controls where an engineer might ponder between using this or a different system. It simply is unlikely to be a consideration for most systems. However, many of us are placed in situations where not all the equipment is new and modern, and for those engineers, an insight into BCD may prove to be a necessary skill in using legacy interfaces.