Hydrogen ion activity in aqueous (water-solvent) solutions is a very important parameter for a wide variety of industrial processes. A number of reactions important to chemical processing are inhibited or significantly slowed if the hydrogen ion activity of a solution lies outside a narrow range. Some additives used in water treatment processes (e.g. flocculants) will fail to function efficiently if the hydrogen ion activity in the water is not kept within a certain range. Alcohol and other fermentation processes strongly depend on tight control of hydrogen ion activity, as an incorrect level of ion activity will not only slow production but may also spoil the product. The concentration of active hydrogen ions in a solution is always measured on a logarithmic scale, and referred to as pH.
[pH]
pH is mathematically defined as the negative common logarithm of active hydrogen ion concentration in a solution. Hydrogen ion concentration is expressed as a molarity (number of moles of ions per liter of total liquid solution volume), with “pH” being the unit of measurement for the logarithmic result:
\[\hbox{pH} = - \log [\hbox{H}^{+}]\]
For example, an aqueous solution with an active hydrogen concentration of 0.00044 \(M\) has a pH value of 3.36 pH.
Water is a covalent compound, and so there is little ionization of water molecules in liquid form. Most of the molecules in a sample of pure water remain as whole molecules (H\(_{2}\)O) while a very small percentage ionize into positive hydrogen ions (H\(^{+}\)) and negative hydroxyl ions (OH\(^{-}\)). The mathematical product of hydrogen and hydroxyl ion molarity in water is known as the ionization constant (\(K_w\)), and its value varies with temperature:
\[K_w = [\hbox{H}^{+}] \times [\hbox{OH}^{-}]\]
At 25 degrees Celsius (room temperature), the value of \(K_w\) is very nearly equal to \(1.0 \times 10^{-14}\). Since each one of the water molecules that does ionize in this absolutely pure water sample separates into exactly one hydrogen ion (H\(^{+}\)) and one hydroxyl ion (OH\(^{-}\)), the molarities of hydrogen and hydroxyl ions must be equal to each other. The equality between hydrogen and hydroxyl ions in a pure water sample means that pure water is neutral, and that the molarity of hydrogen ions is equal to the square root of \(K_w\):
\[[\hbox{H}^+] = \sqrt{K_w} = \sqrt{1.0 \times 10^{-14}} = 1.0 \times 10^{-7} \> M\]
Since we know pH is defined as the negative logarithm of hydrogen ion activity, and we can be assured all hydrogen ions present in a pure water sample will be “active” since there are no other positive ions to interfere with them, the pH value for water at 25 degrees Celsius is:
\[\hbox{pH of pure water at 25 } ^o\hbox{C} = - \log (1.0 \times 10^{-7} \> M) = 7.0 \hbox{ pH}\]
As the temperature of a pure water sample changes, the ionization constant changes as well. Increasing temperature causes more of the water molecules to ionize into H\(^{+}\) and OH\(^{-}\) ions, resulting in a larger \(K_w\) value and a lower pH value. The following table shows \(K_w\) and pH values for pure water at different temperatures:
| Temperature | $K_W$ | pH |
|---|---|---|
| 0 $^{o}$C | 1.139 $\times$ $10^{-15}$ | 7.47 pH |
| 5 $^{o}$C | 1.846 $\times$ $10^{-15}$ | 7.37 pH |
| 10 $^{o}$C | 2.920 $\times$ $10^{-15}$ | 7.27 pH |
| 15 $^{o}$C | 4.505 $\times$ $10^{-15}$ | 7.17 pH |
| 20 $^{o}$C | 6.809 $\times$ $10^{-15}$ | 7.08 pH |
| 25 $^{o}$C | 1.008 $\times$ $10^{-14}$ | 6.998 pH |
| 30 $^{o}$C | 1.469 $\times$ $10^{-14}$ | 6.92 pH |
| 35 $^{o}$C | 2.089 $\times$ $10^{-14}$ | 6.84 pH |
| 40 $^{o}$C | 2.919 $\times$ $10^{-14}$ | 6.77 pH |
| 45 $^{o}$C | 4.018 $\times$ $10^{-14}$ | 6.70 pH |
| 50 $^{o}$C | 5.474 $\times$ $10^{-14}$ | 6.63 pH |
| 55 $^{o}$C | 7.296 $\times$ $10^{-14}$ | 6.57 pH |
| 60 $^{o}$C | 9.614 $\times$ $10^{-14}$ | 6.51 pH |
This means that while any pure water sample is neutral (an equal number of positive hydrogen ions and negative hydroxyl ions) at any temperature, the pH value of pure water actually changes with temperature, and is only equal to 7.0 pH at one particular (“standard”) temperature: 25 \(^{o}\)C. Based on the \(K_w\) values shown in the table, pure water will be 6.51 pH at 60 \(^{o}\)C and 7.47 pH at freezing.
If we add an electrolyte to a sample of pure water, molecules of that electrolyte will separate into positive and negative ions. If the positive ion of the electrolyte happens to be a hydrogen ion (H\(^{+}\)), we call that electrolyte an acid. If the negative ion of the electrolyte happens to be a hydroxyl ion (OH\(^{-}\)), we call that electrolyte a caustic, or alkaline, or base. Some common acidic and alkaline substances are listed here, showing their respective positive and negative ions in solution:
Sulfuric acid is an acid (produces H\(^{+}\) in solution)
H\(_{2}\)SO\(_{4}\) \(\to\) 2H\(^{+}\) + SO\(_{4}\)\(^{2-}\)
Nitric acid is an acid (produces H\(^{+}\) in solution)
HNO\(_{3}\) \(\to\) H\(^{+}\) + NO\(_{3}\)\(^{-}\)
Hydrocyanic acid is an acid (produces H\(^{+}\) in solution)
HCN \(\to\) H\(^{+}\) + CN\(^{-}\)
Hydrofluoric acid is an acid (produces H\(^{+}\) in solution)
HF \(\to\) H\(^{+}\) + F\(^{-}\)
Lithium hydroxide is a caustic (produces OH\(^{-}\) in solution)
LiOH \(\to\) Li\(^{+}\) + OH\(^{-}\)
Potassium hydroxide is a caustic (produces OH\(^{-}\) in solution)
KOH \(\to\) K\(^{+}\) + OH\(^{-}\)
Sodium hydroxide is a caustic (produces OH\(^{-}\) in solution)
NaOH \(\to\) Na\(^{+}\) + OH\(^{-}\)
Calcium hydroxide is a caustic (produces OH\(^{-}\) in solution)
Ca(OH)\(_{2}\) \(\to\) Ca\(^{2+}\) + 2OH\(^{-}\)
When an acid substance is added to water, some of the acid molecules dissociate into positive hydrogen ions (H\(^{+}\)) and negative ions (the type of negative ions depending on what type of acid it is). This increases the molarity of hydrogen ions (the number of moles of H\(^{+}\) ions per liter of solution), therefore driving the pH value of the solution down to a smaller number. For example, a sample of acid added to a sample of neutral water at room temperature (7 pH) will drive the pH value down below 7 due to the increasing molarity of hydrogen ions in the solution. The addition of hydrogen ions to the solution also decreases the molarity of hydroxyl ions (the number of moles of OH\(^{-}\) ions per liter of solution) because some of the water’s OH\(^{-}\) ions combine with the acid’s H\(^{+}\) ions to form deionized water molecules (H\(_{2}\)O).
If an alkaline substance (otherwise known as a caustic, or a base) is added to water, some of the alkaline molecules dissociate into negative hydroxyl ions (OH\(^{-}\)) and positive ions (the type of positive ions depending on what type of alkaline it is). This increases the molarity of OH\(^{-}\) ions in the solution, as well as decreases the molarity of hydrogen ions (again, because some of the caustic’s OH\(^{-}\) ions combine with the water’s H\(^{+}\) ions to form deionized water molecules, H\(_{2}\)O). This decrease in hydrogen ion molarity will raise the pH value of the solution. For example, if we were to add a sample of caustic to a sample of neutral water at room temperature (7 pH), the pH of the solution would increase with the decreasing hydrogen ion molarity.
The result of this complementary effect (increasing one type of water ion, decreasing the other) keeps the overall ionization constant relatively constant, at least for dilute solutions. In other words, the addition of an acid or a caustic to water may change [H\(^{+}\)], but it has little effect on \(K_w\).
A simple way to envision this effect is to think of a laboratory balance scale, balancing the number of hydrogen ions in a solution against the number of hydroxyl ions in the same solution:
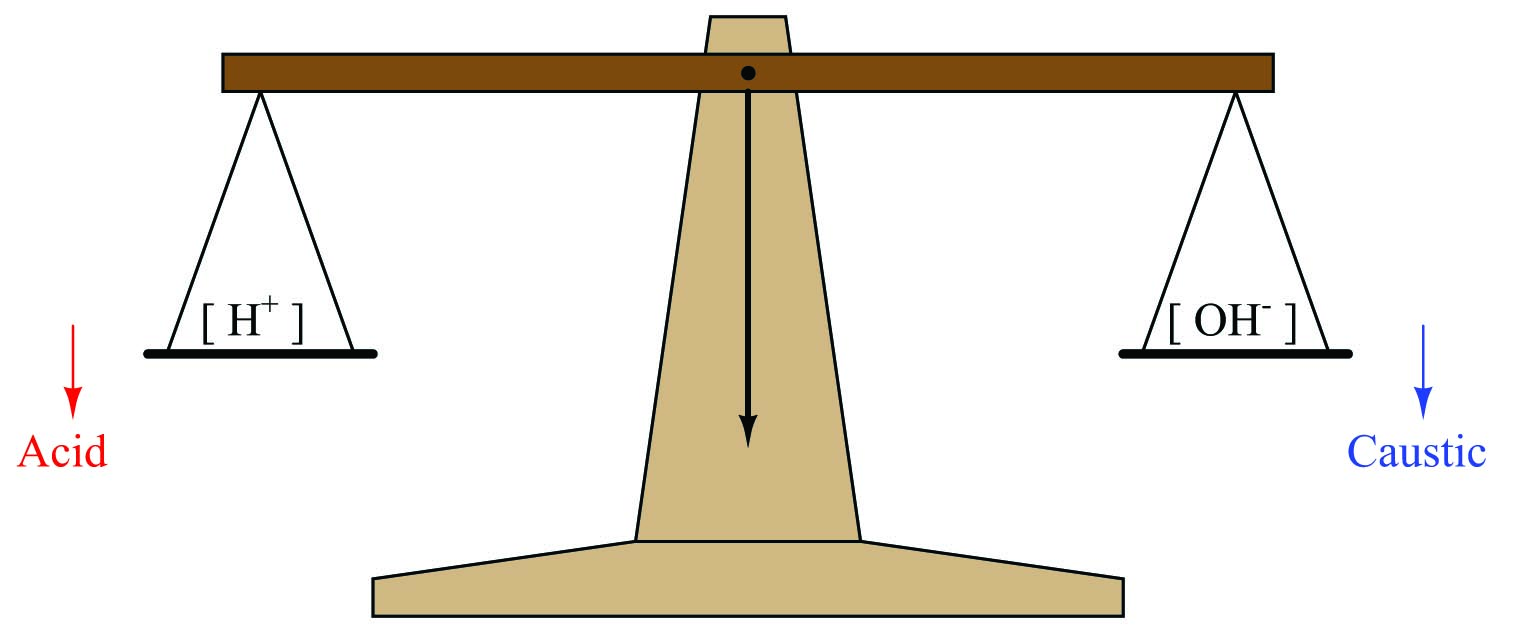
When the solution is pure water, this imaginary scale is balanced (neutral), with [H\(^{+}\)] = [OH\(^{-}\)]. Adding an acid to the solution tips the scale to the left (lower pH value), while adding a caustic to the solution tips the scale to the right (higher pH value).
If an electrolyte has no effect on either the hydrogen and hydroxyl ion activity of an aqueous solution, we call it a salt. The following is a list of some common salts, showing their respective ions in solution:
Potassium chloride is a salt (produces neither H\(^{+}\) nor OH\(^{-}\) nor O\(^{2-}\) in solution)
KCl \(\to\) K\(^{+}\) + Cl\(^{-}\)
Sodium chloride is a salt (produces neither H\(^{+}\) nor OH\(^{-}\) nor O\(^{2-}\) in solution)
NaCl \(\to\) Na\(^{+}\) + Cl\(^{-}\)
Zinc sulfate is a salt (produces neither H\(^{+}\) nor OH\(^{-}\) nor O\(^{2-}\) in solution)
ZnSO\(_{4}\) \(\to\) Zn\(^{2+}\) + SO\(_{4}\)\(^{2-}\)
The addition of a salt to an aqueous solution should have no effect on pH, because the ions created neither add to nor take away from the hydrogen ion activity.
Acids and caustics tend to neutralize one another, the hydrogen ions liberated by the acid combining (and canceling) with the hydroxyl ions liberated by the caustic. This process is called pH neutralization, and it is used extensively to adjust the pH value of solutions. If a solution is too acidic, just add caustic to raise its pH value. If a solution is too alkaline, just add acid to lower its pH value.
The result of a perfectly balanced mix of acid and caustic is deionized water (H\(_{2}\)O) and a salt formed by the combining of the acid’s and caustic’s other ions. For instance, when hydrochloric acid (HCl) and potassium hydroxide (KOH) neutralize one another, the result is water (H\(_{2}\)O) and potassium chloride (KCl), a salt. This production of salt is a necessary side-effect of pH neutralization, which may require addressing in later stages of solution processing. Such neutralizations are exothermic, owing to the decreased energy states of the hydrogen and hydroxyl ions after combination. Mixing of pure acids and caustics together without the presence of substantial quantities of water (as a solvent) is often violently exothermic, presenting a significant safety hazard to anyone near the reaction.
Both acidic and caustic solutions pose safety hazards to human and animal life. Concentrated acids will cause burns to living tissue, while concentrated caustics chemically reduce fat within tissue to soap. These hazards are not just related to external skin contact, but also to internal contact in the form of ingestion or inhalation.
For more information on pH and its measurement, refer to the beginning of the page discussing different technologies for measuring the concentration of hydrogen ions in liquid solutions.