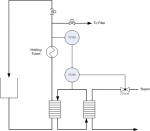
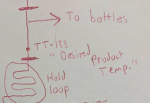
I work at a food processing plant that requires that we hold a liquid product at a certain temperature while it is travelling through piping. A Rockwell PIDE controller controls this process, which is essentially a heat exchanger that opens a valve (0-100%) to release steam, heating the product in a triple tube heater to its desired set point. If the product does not reach this set temperature by the time it reaches the end of the hold pipe, then it is sent back to the product hold tank to be recirculated.
The main problem: the current system is overheating our product by ~20 degrees F, which is essentially burning it, incurring build-up on probes and affecting quality.
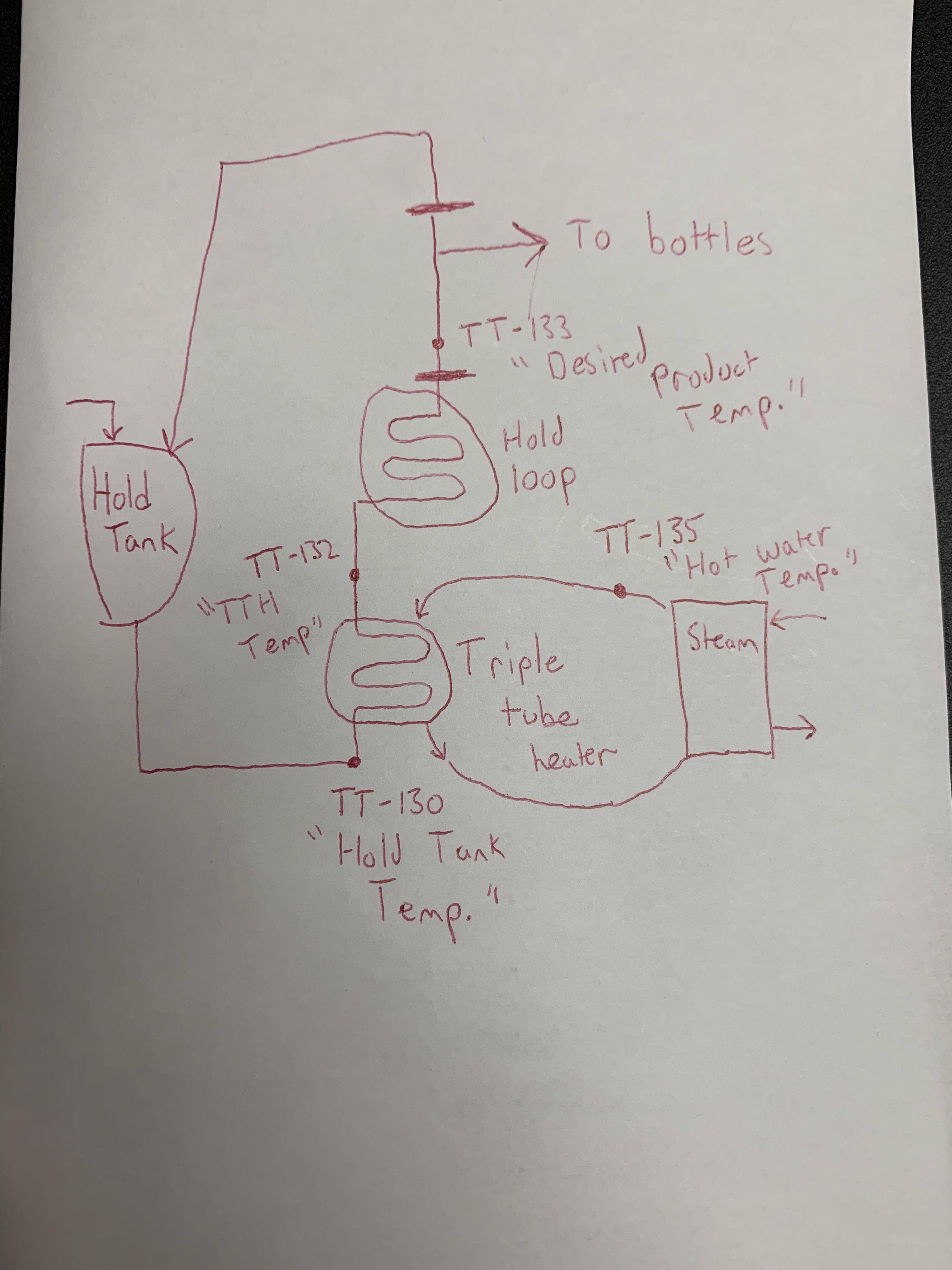
Above is a brief drawing of what the system looks like. TT-130 is the incoming product temperature, TT-132 is what the product is being heated to by the hot water, TT-135 is the hot water temperature (which is controlled by opening/closing a valve), TT-133 is what the finished product temperature is (if the temperature set point is reached, release to bottles.. if not recirculate).
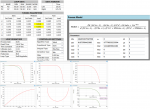
Currently, our PID controller is set to Kp = 4, Ki = 4, Kd = 0. Clearly there is some overshoot, and because the process is so slow and delicate, it is not in our best interest to use trial and error to figure out the best parameters. Below is a plot I created in MATLAB to try and model our plant. The empirical data is normalized (TT-132 "Triple tube heater temp"/Set point) and shows many oscillations. Note the time (in seconds).. the initial rise time is approx. 10 minutes.
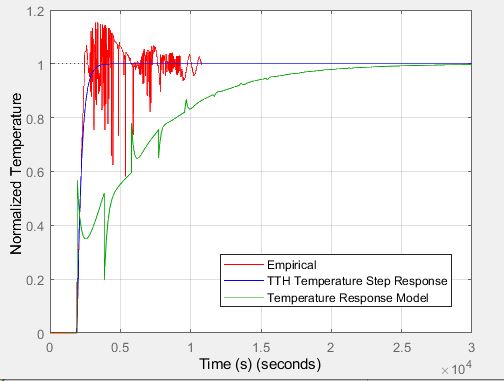
The empirical plot includes the current controller settings (p = 4, i = 4, d = 0) during a start up period. The blue graph is a first-order-plus-deadtime representation of the heat exchanger (taking 't' at 28.3 % and 63.2% of the final value then finding tau/theta to create a transfer function as the plant model). The following is the code used to execute the green plot, which is my attempt at using an ITAE PID controller alongside the calculated transfer function.

Obviously this response isn't exactly desirable for our system.. I want to remove the overshoot (from 220 degrees F to our setpoint of 200 degrees F) without the risk of using a trial and error method. Am I modelling this plant properly? What is a strategy I could employ that I could use to create an accurate plant model? Do IAE/ITAE formulas work for such a slow process? I noticed that the Ti and Td values were fairly large, while Kc was always <1.
Any guidance on this topic would be fantastic.. controls are not my strong suit.
The main problem: the current system is overheating our product by ~20 degrees F, which is essentially burning it, incurring build-up on probes and affecting quality.

Above is a brief drawing of what the system looks like. TT-130 is the incoming product temperature, TT-132 is what the product is being heated to by the hot water, TT-135 is the hot water temperature (which is controlled by opening/closing a valve), TT-133 is what the finished product temperature is (if the temperature set point is reached, release to bottles.. if not recirculate).
Currently, our PID controller is set to Kp = 4, Ki = 4, Kd = 0. Clearly there is some overshoot, and because the process is so slow and delicate, it is not in our best interest to use trial and error to figure out the best parameters. Below is a plot I created in MATLAB to try and model our plant. The empirical data is normalized (TT-132 "Triple tube heater temp"/Set point) and shows many oscillations. Note the time (in seconds).. the initial rise time is approx. 10 minutes.

The empirical plot includes the current controller settings (p = 4, i = 4, d = 0) during a start up period. The blue graph is a first-order-plus-deadtime representation of the heat exchanger (taking 't' at 28.3 % and 63.2% of the final value then finding tau/theta to create a transfer function as the plant model). The following is the code used to execute the green plot, which is my attempt at using an ITAE PID controller alongside the calculated transfer function.

Obviously this response isn't exactly desirable for our system.. I want to remove the overshoot (from 220 degrees F to our setpoint of 200 degrees F) without the risk of using a trial and error method. Am I modelling this plant properly? What is a strategy I could employ that I could use to create an accurate plant model? Do IAE/ITAE formulas work for such a slow process? I noticed that the Ti and Td values were fairly large, while Kc was always <1.
Any guidance on this topic would be fantastic.. controls are not my strong suit.