First, let us review some of the properties of differentials and derivatives, referencing the expression and graph shown below:

Next, let us review some of the properties of integrals, referencing the expression and graph shown below:

Just as division and multiplication are inverse mathematical functions (i.e. one “un-does” the other), differentiation and integration are also inverse mathematical functions. The two examples of propane gas flow and mass measurement highlighted in the previous sections illustrates this complementary relationship. We may use differentiation with respect to time to convert a mass measurement (\(m\)) into a mass flow measurement (\(W\), or \(dm \over dt\)). Conversely, we may use integration with respect to time to convert a mass flow measurement (\(W\), or \(dm \over dt\)) into a measurement of mass gained or lost (\(\Delta m\)).
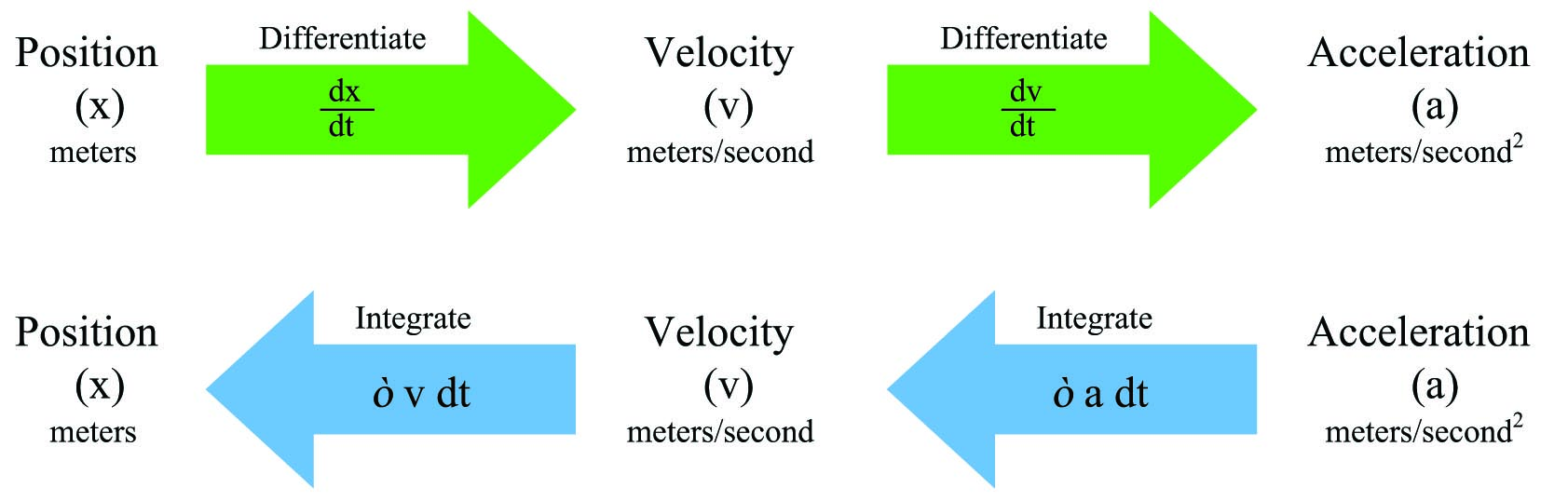
Likewise, the common examples of position (\(x\)), velocity (\(v\)), and acceleration (\(a\)) used to illustrate the principle of differentiation are also related to one another by the process of integration. Reviewing the derivative relationships:
\[v = {dx \over dt} \hbox{\hskip 30pt Velocity is the derivative of position with respect to time}\]
\[a = {dv \over dt} \hbox{\hskip 30pt Acceleration is the derivative of velocity with respect to time}\]
Now, expressing position and velocity as integrals of velocity and acceleration, respectively11:
\[x = \int v \> dt \hbox{\hskip 30pt Position is the integral of velocity with respect to time}\]
\[v = \int a \> dt \hbox{\hskip 30pt Velocity is the integral of acceleration with respect to time}\]
Differentiation and integration may be thought of as processes transforming these quantities into one another. Note the transformation of units with each operation – differentiation always divides while integration always multiplies:
The inverse nature of these two calculus operations is codified in mathematics as the Fundamental Theorem of Calculus, shown here:
\[{d \over dx} \left[ \int_a^b f(x) \> dx \right] = f(x)\]
What this equation tells us is that the derivative of the integral of any continuous function is that original function. In other words, we can take any mathematical function of a variable that we know to be continuous over a certain range – shown here as \(f(x)\), with the range of integration starting at \(a\) and ending at \(b\) – integrate that function over that range, then take the derivative of that result and end up with the original function. By analogy, we can take the square-root of any quantity, then square the result and end up with the original quantity, because these are inverse functions as well.
A feature of this book which may be helpful to your understanding of derivatives, integrals, and their relation to each other is found in an Appendix section (Appendix [animation_calculus_tankfilling] beginning on page ). In this section, a series of illustrations provides a simple form of animation you may “flip” through to view the filling and emptying of a water storage tank, with graphs showing stored volume (\(V\)) and volumetric flow rate (\(Q\)). Since flow rate is the time-derivative of volume (\(Q = {dV \over dt}\)) and volume change is the time-integral of volumetric flow rate (\(\Delta V = \int Q \> dt\)), the animation demonstrates both concepts in action.