To review, voltage is the measure of potential energy available to electric charges. Current is the uniform drifting of electric charges in response to a voltage. We can have a voltage without having a current, but we cannot have a current without first having a voltage to motivate it. Current without voltage would be equivalent to motion without a motivating force.
When electric charges move through a material such as metal, they will naturally encounter some friction, just as fluid moving through a pipe will inevitably encounter friction. We have a name for this friction to electrical charge motion: resistance. Like voltage and current, resistance has its own special unit of measurement: the ohm, named in honor of the German physicist Georg Simon Ohm.
At this point it would be good to summarize and compare the symbols and units we use for voltage, current, and resistance:
| Quantity | Symbol | Unit | Abbreviation |
| Voltage | \(V\) (or \(E\)) | Volt | V |
| Current | \(I\) | Ampere (or Amp) | A |
| Resistance | \(R\) | Ohm | \(\Omega \) |
Ohm defined resistance as the mathematical ratio between applied voltage and resulting current. This formula become known as Ohm’s Law, perhaps the most basic formula in all of electrical science (shown here in three different forms, each one solving for a different variable):
\[R = {V \over I} \hskip 30pt V = IR \hskip 30pt I = {V \over R}\]
Verbally expressed, resistance is how much voltage it takes to force a certain rate of current through a conductive material. Many materials have relatively stable resistances, while others do not. Devices called resistors are sold which are manufactured to possess a very precise amount of resistance, for the purpose of limiting current in circuits (among other things).
Here is an example of Ohm’s Law in action: calculate the amount of current in a circuit with a voltage source of 25 V and a total resistance of 3500 \(\Omega\). Taking 25 volts and dividing by 3500 ohms, you should arrive at a result of 0.007143 amperes, or 7.143 milliamperes (7.143 mA).
One of the most challenging aspect of Ohm’s Law is remembering to keep all variables in context. This is a common problem for many students when studying physics as well: none of the equations learned in a physics class will yield the correct results unless all the variables relate to the same object or situation. For instance, it would make no sense to try to calculate the kinetic energy of a moving object (\(E = {1 \over 2}mv^2\)) by taking the mass of one object (\(m\)) and multiplying it by the square of the velocity of some other object (\(v^2\)). Likewise, with Ohm’s Law, we must make sure the voltage, current, and resistance values we are using all relate to the same portion of the same circuit.
If the circuit in question has only one source of voltage, one resistance, and one path for current, we cannot mis-apply Ohm’s Law. Expressing the previous example in a schematic diagram:

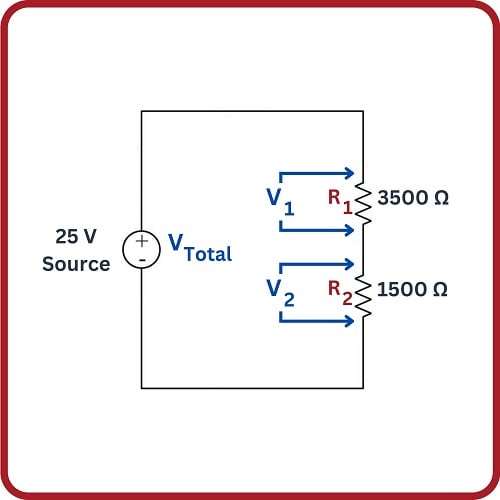
However, if we look at a more complex circuit, we encounter the potential for mis-application of Ohm’s Law because we have multiple resistances in the circuit rather than just one resistance:

Which resistance do we use to calculate current in this circuit? Do we divide our 25 volts by 3500 ohms like we did last time, or do we divide it by 1500 ohms, or something entirely different? The answer to this question lies in the identification of voltages and currents. We know that the 25 volt potential will be impressed across the total of the two resistances \(R_1\) and \(R_2\), and since there is only one path for current they must share the same current. Thus, we actually have three voltages (\(V_1\), \(V_2\), and \(V_{total}\)), three resistances (\(R_1\), \(R_2\), and \(R_{total}\)), and only one current (\(I\)):
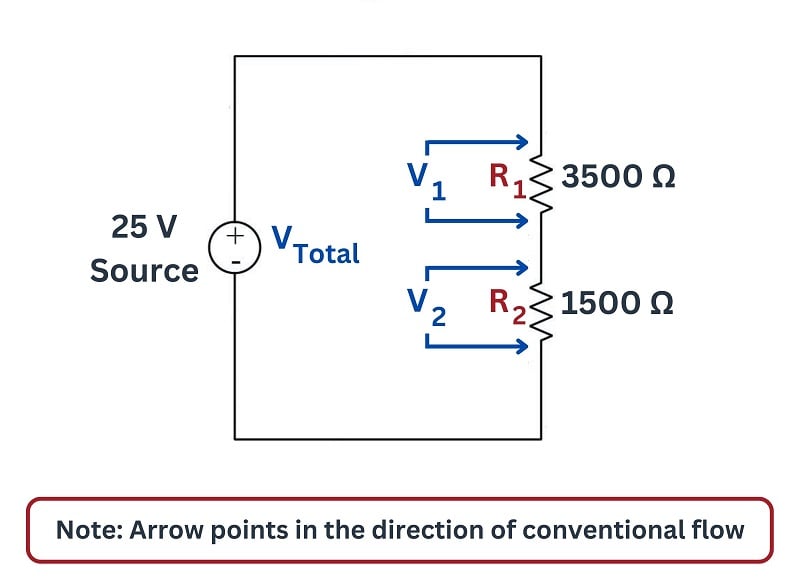
Using the \(V = IR\) form of Ohm’s Law to relate these three voltages (\(V_1\), \(V_2\), and \(V_{total}\)) to the one current (\(I\)), we end up with three equations for this circuit:
\[V_{1} = I R_{1}\]
\[V_{2} = I R_{2}\]
\[V_{total} = I R_{total} = I (R_1 + R_2)\]
We can only solve for one unknown variable at a time in any equation. This means we cannot solve for \(V_1\) yet, because although we do know the value of resistor \(R_1\) (3500 ohms), we do not yet know the circuit’s current (\(I\)). Likewise for \(V_2\), because we do not yet know the value of \(I\). However, the third equation is solvable, since we happen to know the total voltage as well as both resistor values, leaving circuit current \(I\) as the only unknown variable. Manipulating this equation and solving for \(I\):
\[I = {V_{total} \over R_{total}} = {V_{total} \over R_1 + R_2}\]
\[{25 \hbox{ V}\over 3500 \> \Omega + 1500 \> \Omega} = 0.005 \hbox{ A} = 5 \hbox{ mA}\]
Now that we know the amount of current in this circuit, we may solve for \(V_1\) and \(V_2\) in the other equations to find that the voltage across resistor \(R_1\) is 17.5 volts, and that the voltage across resistor \(R_2\) is 7.5 volts.
REVIEW: