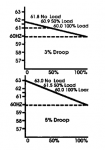
PungentReindeerKing is correct. The WORST mistake most people make--especially with GE-design heavy duty gas turbines--is to operate in a mode that's always trying to maintain a load setpoint, and adjusting the turbine speed reference in doing so. In GE-speak it's called Pre-Selected Load Control, and in it's most basic form what happens when the grid frequency deviates from normal which causes the actual speed to deviate from normal is that Droop Speed Control changes the fuel flow-rate because the speed error changes, which changes the actual load--making it deviate from the setpoint--and then Pre-Selected Load Control changes the turbine speed reference to try to return the load to the setpoint, and from there it's a horse race! In other words, the load fluctuates, sometimes by a lot. And this in turn contributes to the grid instability--making it worse!
GE will let Customers pay for a fix for their (GE's) problem--it's called PFR, Primary Frequency Response. And, it will sense a deviation in actual speed--which is an indicator of a grid frequency problem--and will temporarily disable Pre-Selected Load Control so that Droop Speed Control can do what it's supposed to do. It works; sort of. It's just a band-aid, actually.
In reality, no one really needs to operate with Pre-Selected Load Control enabled. Why? Because once the desired load is achieved (by the operator raising or lowering the load to the desired value) and stops using the RAISE- and/or LOWER SPEED/LOAD buttons the turbine speed reference stops changing. So, the speed error stops changing. And when the grid is stable, the speed error doesn't change. So, the fuel flow-rate doesn't change. So, the load stays the same. In most cases, the load is actually more stable than if Pre-Selected Load Control is not active!
But, no one can convince operators, or their supervision, that the unit will remain stable if Pre-Selected Load Control isn't active. Not no how. Not no way. They won't try it for one minute (60 seconds). Or even for 30 seconds. Because the just KNOW that if Pre-selected Load Control isn't active the unit load is going to drift, or worse--it's going to jump. And even worse, it's going to be completely unstable. And someone will lose their job. So, good luck trying to convince anyone to try operating the unit without Pre-Selected Load Control inactive. It just won't happen.
So, what happens when the grid frequency does deviate from rated? Well, if the unit has been outfitted with PFR and Pre-Selected Load Control is active, the fun begins. Not only is the unit load changing because of the grid frequency instability, but it's even more unstable because of the Pre-Selected Load Control fighting with Droop Speed Control. Which only makes the grid frequency more unstable.
And, those same operators and their supervision who believe in the heart and soul that the unit will be unstable if not operated with Pre-Selected Load Control active also believe in the heart and soul that their unit should NOT change it's load under any circumstances--even if the grid frequency is unstable! So, the Mark* is deemed to be the cause of the problem--when it's only making the problem worse because of the way it's being operated.
But, good luck convincing anyone of that. "If GE had wanted Pre-Selected Load Control to self-cancel when the desired load setpoint was reached, they would have programmed it to work that way!" That's what Pre-Selected Load Control was designed to do--make it easy for the operator to change load without a lot of button-pushing, or handle twisting, or clicking. It was intended that once the setpoint was reached, the function would be cancelled--because, again, when the speed reference and the actual speed are both not changing, then the speed error is not changing, and the fuel flow-rate will not change, and the load will not change. BUT, they just forgot to do that one little thing--automatically cancel Pre-Selected Load Control when the desired setpoint was reached. They left that up to the operator, but, operators simply can't be bothered to take that extra step--especially when they firmly believe if they do the unit will go unstable, and someone will lose their job.
Anyway, as for the rest of what PungentReindeerKing wrote, it's all true. A lot of these functions are "layered" on top of each other (in the way Pre-Selected Load Control is layered on top of Droop Speed Control) and they need to be tuned or adjusted to all work together properly. In some cases, they can't be made to work together--but that doesn't stop people from continuing to try to force them to work together. And, in the end--it's always the Mark*'s fault that they can't work together.
Such is life.
GE will let Customers pay for a fix for their (GE's) problem--it's called PFR, Primary Frequency Response. And, it will sense a deviation in actual speed--which is an indicator of a grid frequency problem--and will temporarily disable Pre-Selected Load Control so that Droop Speed Control can do what it's supposed to do. It works; sort of. It's just a band-aid, actually.
In reality, no one really needs to operate with Pre-Selected Load Control enabled. Why? Because once the desired load is achieved (by the operator raising or lowering the load to the desired value) and stops using the RAISE- and/or LOWER SPEED/LOAD buttons the turbine speed reference stops changing. So, the speed error stops changing. And when the grid is stable, the speed error doesn't change. So, the fuel flow-rate doesn't change. So, the load stays the same. In most cases, the load is actually more stable than if Pre-Selected Load Control is not active!
But, no one can convince operators, or their supervision, that the unit will remain stable if Pre-Selected Load Control isn't active. Not no how. Not no way. They won't try it for one minute (60 seconds). Or even for 30 seconds. Because the just KNOW that if Pre-selected Load Control isn't active the unit load is going to drift, or worse--it's going to jump. And even worse, it's going to be completely unstable. And someone will lose their job. So, good luck trying to convince anyone to try operating the unit without Pre-Selected Load Control inactive. It just won't happen.
So, what happens when the grid frequency does deviate from rated? Well, if the unit has been outfitted with PFR and Pre-Selected Load Control is active, the fun begins. Not only is the unit load changing because of the grid frequency instability, but it's even more unstable because of the Pre-Selected Load Control fighting with Droop Speed Control. Which only makes the grid frequency more unstable.
And, those same operators and their supervision who believe in the heart and soul that the unit will be unstable if not operated with Pre-Selected Load Control active also believe in the heart and soul that their unit should NOT change it's load under any circumstances--even if the grid frequency is unstable! So, the Mark* is deemed to be the cause of the problem--when it's only making the problem worse because of the way it's being operated.
But, good luck convincing anyone of that. "If GE had wanted Pre-Selected Load Control to self-cancel when the desired load setpoint was reached, they would have programmed it to work that way!" That's what Pre-Selected Load Control was designed to do--make it easy for the operator to change load without a lot of button-pushing, or handle twisting, or clicking. It was intended that once the setpoint was reached, the function would be cancelled--because, again, when the speed reference and the actual speed are both not changing, then the speed error is not changing, and the fuel flow-rate will not change, and the load will not change. BUT, they just forgot to do that one little thing--automatically cancel Pre-Selected Load Control when the desired setpoint was reached. They left that up to the operator, but, operators simply can't be bothered to take that extra step--especially when they firmly believe if they do the unit will go unstable, and someone will lose their job.
Anyway, as for the rest of what PungentReindeerKing wrote, it's all true. A lot of these functions are "layered" on top of each other (in the way Pre-Selected Load Control is layered on top of Droop Speed Control) and they need to be tuned or adjusted to all work together properly. In some cases, they can't be made to work together--but that doesn't stop people from continuing to try to force them to work together. And, in the end--it's always the Mark*'s fault that they can't work together.
Such is life.