
In any closed circuit, the current exiting and entering the power supply must be equal. Differential current protection, much like a ground-fault interrupter (GFI), measures incoming and exiting current from all three phases, stopping the circuit in case of any imbalance, no matter how long it persists.
One of the fundamental laws of electric circuits is Kirchhoff’s Current Law, which states the algebraic sum of all currents at a circuit node (junction) must be zero. A simpler way of stating this is to say “what goes in must come out.” We may exploit this principle to provide another form of protection against certain faults in electric circuits, by measuring the amount of current entering and exiting a circuit component, then tripping a circuit breaker if those two currents ever fail to match.
An important advantage of differential protection as compared to either instantaneous- or time-overcurrent protection is that it is far more sensitive and faster-acting. Unlike either form of overcurrent protection, which picks up only if current exceeds the maximum rating of the conductors, differential protection is able to pick up at far lower levels of current because Kirchhoff’s Current Law predicts that any amount of current imbalance, for any length of time, is abnormal. Lower pick-up thresholds along with no time delay means that differential protection is able to take action sooner than any form of overcurrent protection can, thereby limiting equipment damage by clearing the fault in a shorter amount of time.
Suppose we were to measure the amount of current at both ends of every phase winding in a three-phase generator, shown in the following diagram:

Like most large power generators, this unit brings both terminals of each phase winding to external points so that they may be connected in either a Wye or a Delta configuration as desired. In this particular case, the generator’s windings are Wye-connected. So long as we measure current going in and out of each winding individually, it matters little whether those generator windings are Wye- or Delta-connected.
If the circuit is exactly as drawn above, the amount of current entering and exiting each phase winding must be the same in accordance with Kirchhoff’s Current Law. That is to say:
\[I_{A1} = I_{A2} \hskip 30pt I_{B1} = I_{B2} \hskip 30pt I_{C1} = I_{C2} \hskip 30pt\]
Suppose now that one of the turns within the “C” phase winding were to accidentally contact the generator’s metal frame, such as what might happen as a result of insulation damage. This ground fault will cause a third path for current in the faulted winding. \(I_{C1}\) and \(I_{C2}\) will now be imbalanced by an amount equal to the fault current \(I_F\):

Another fault detectable by Kirchhoff’s Current Law is a phase-to-phase winding fault, where current flows from one winding to another. In this example, a fault between B and C phases in the generator upsets the balance of incoming and outgoing currents for both phases:
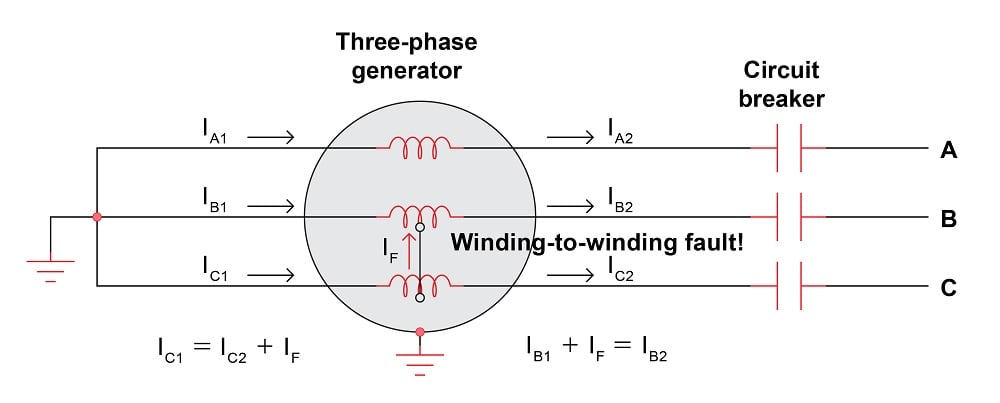
It should be noted that the magnitude of a ground fault or a winding-to-winding fault current might not be large enough to pose an overcurrent threat to the generator, yet the very existence of a current imbalance in any phase proves the winding is damaged. In other words, this is a type of system fault that would not necessarily be detected by an overcurrent (50/51) relay, and so must be detected by some other means.
The relay type designated for this task is called a differential current relay. The ANSI/IEEE number code for differential protection is 87. Differential voltage relays also exist, with the same “87” ANSI/IEEE designation, making it necessary to specify whether the differential quantity in question is voltage or current whenever mentioning an “87” relay.
A simple form of differential current protection for this generator may be implemented by connecting CTs on either side of each winding to operating coils of an electromechanical relay like this. For the sake of simplicity, protection for only one phase winding (C) of the generator will be shown. A practical differential current protective relay system would monitor current through all six stator wires on the generator, comparing currents in and out of every phase:

If the CT primary currents \(I_{C1p}\) and \(I_{C2p}\) are equal and the CT ratios are equal, the CT secondary currents \(I_{C1s}\) and \(I_{C2s}\) will be equal as well. The result will be zero current through the operating coil (OC) of the differential relay.
If, however, a fault to ground or to an adjacent winding were to develop anywhere within the generator’s “C” stator winding, the primary currents of the two CTs will become unequal, causing unequal secondary currents, thereby causing a substantial amount of current to flow through the differential relay’s operate coil (OC). If this current is sufficient to cause the differential relay to “pick up”, the relay will send a signal commanding the generator’s circuit breaker to trip.
Even with the relay’s pickup value biased to avoid unnecessary tripping, it is still possible that a heavy phase current demanded from the generator may cause the differential relay to trip, due to the impossibility of a perfect match between the two “C” phase current transformers. Any mismatch between these two CTs will result in an inequality of secondary currents that will become larger as phase current grows in magnitude. Large, harmonic-rich inrush currents occasionally experienced when a large power transformer is initially energized may also cause false trips in this simple form of differential protection. We do not wish this differential relay to trip for any condition but an internal generator fault in its phase winding, and so a modification is necessary to provide a different operating characteristic.
If we modify the relay to have three coils, one to move its mechanism in the trip direction, and two to help “restrain” its mechanism (working to hold the mechanism in its normal operating position), we may connect these coils in such a way that the two restraint coils (RC) are energized by the two CT secondary currents, while the operating coil only sees the difference between the two CT secondary currents. We refer to this scheme as a restrained differential relay, and the former (simpler) design as an unrestrained differential relay:

The general characteristic of a restrained differential relay is to trip on the basis of the differential current exceeding a set percentage of phase current.
This photograph shows three differential relays used to protect the windings of a three-phase generator at a gas turbine power plant. Note how one differential current relay is required to protect each of the generator’s three phases:

Modern digital differential relays typically sense CT signals from all three phases, allowing protection in a single panel-mount unit. Digital protective relays offer much more sophisticated approaches to the problem of false tripping based on mismatches between current transformer pairs and/or harmonic currents. The following graph shows the characteristic for a General Electric model 745 transformer protective relay providing differential current protection:

Not only may the pickup value be adjusted by the user, but also the slope of each line segment on the graph, the height of the “kneepoint” step, etc. Note how the term “restraint” is still used in digital relay configuration, even though it originated in electromechanical relay designs.
It is noteworthy that a form of differential current protection also finds application in American households, where electrical codes require the installation of Ground Fault Current Interruptor (GFCI) protected circuits in areas where contact between electrical appliances and water is likely (e.g. bathrooms, kitchens). GFCI receptacles function by sensing any difference in current between the “hot” and “neutral” conductors carrying current to and from any load plugged into the receptacle:
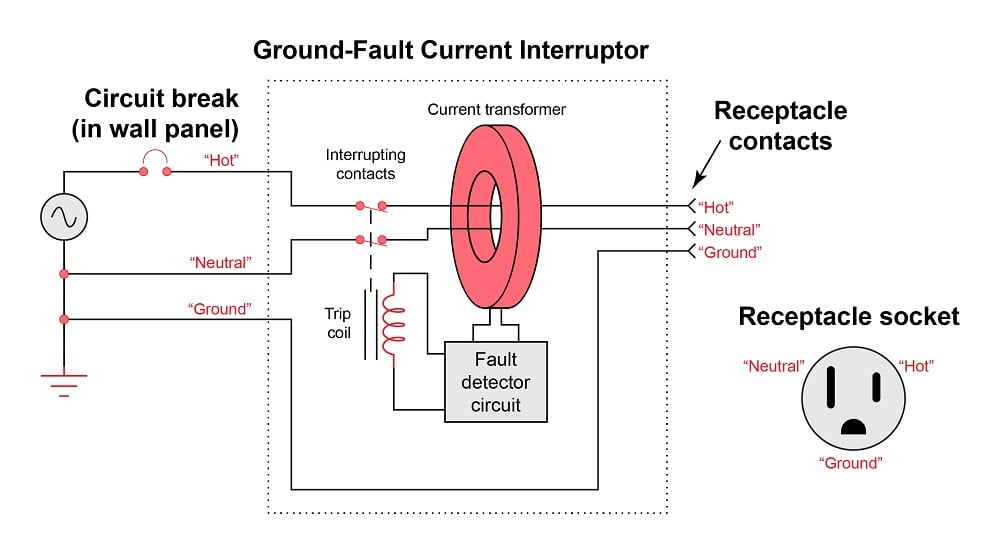
A single current transformer (CT) within the GFCI unit senses any differential current by sensing the net magnetic field around both current-carrying conductors. If the “hot” and “neutral” currents are equal, their opposite directions will produce opposing magnetic fields, with zero net magnetic field sensed by the CT. If, however, a ground fault exists at the load plugged into this receptacle, these two currents will be unequal and the CT will detect a net magnetic field. These protective devices are extraordinarily sensitive, tripping the contacts with differential current values in the milliamp range. This is important, as a ground fault existing in an electrical appliance may very well pass through the body of a person or an animal, in which case mere milliamps may prove harmful or even fatal.
If a GFCI receptacle trips, it may be reset by pressing a “reset” button on its face. GFCI units may also be manually tested by pressing a “test” button also mounted on the front face.
A very important concept in the field of protective relaying is that of protection zones, which is easily explained in the context of differential current relays. Simply defined, a relay’s “protection zone” is the physical range wherein the specified electrical fault may be detected, and thereby any components and connections within the zone may be protected through proper relay action. Overcurrent (50/51) relays discussed in an earlier section of this book do not exhibit well-defined zones of protection, since overcurrent relays pick up on a certain minimum fault current value, not necessarily on any certain fault location. Differential current relays, however, exhibit very clear and unambiguous zones of protection: the area lying between the current-sensing CT pair:
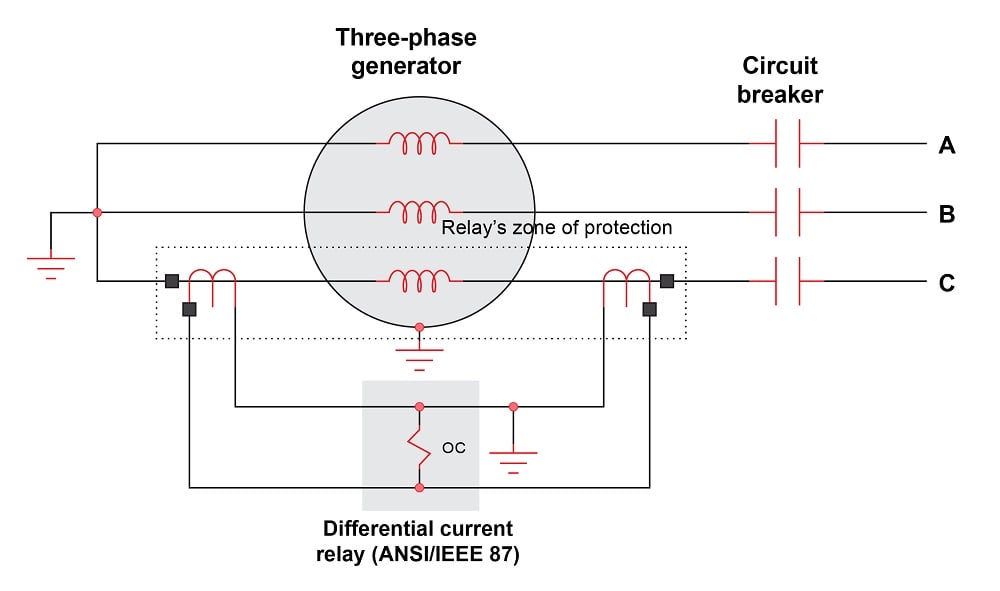
Only a fault within the relay’s protection zone (i.e. an “internal” fault) is capable of forcing the two CTs currents to become unequal. Thanks to Kirchhoff’s Current Law, no fault outside the protection zone (i.e. an “external” fault), no matter how severe, can make the CT primary currents become unequal.
The concept of protection zones is a very important one in protective relaying, and finds application well beyond differential current (87) systems. It is closely related to the concept of selectivity, which means the ability of a protective relay to discriminate between a fault within its own protection zone and one lying outside of its zone. A relay with high selectivity is one capable of ignoring external faults, while a relay with poor selectivity may falsely trip when faced with external faults.
Ground Fault Current-Interrupting (GFCI) household power receptacles also exhibit well-defined zones of protection. In the case of a GFCI the zone of protection is anything plugged in to the receptacle (i.e. to the right of the CT in the diagram):

A common residential wiring practice in the United States is to “daisy-chain” regular receptacles to a GFCI receptacle where water hazards exist, such that all receptacles powered through the GFCI become part of the GFCI’s protection zone. A bathroom wired this way, for example, provides the exact same degree of ground fault protection at all receptacles in the room. If someone were to plug an electric hair dryer into one of those “daisy-chained” receptacles and then accidently drop that appliance into a bathtub full of water, the GFCI would trip and cut power to all of the receptacles just as surely as it would trip if the hair dryer had been plugged directly into the GFCI receptacle itself.
Differential current protection is most practical to implement over short physical distances, such as over the phase windings in a generator or some other power system component, but the fundamental concept is applicable over longer distances as well because Kirchhoff’s Current Law knows no bounds. Consider for example a transmission line spanning miles of distance between two busses, shown in this single-line diagram:

Here, two differential relays control the tripping of circuit breakers (ANSI/IEEE function 52) at each end of the transmission line. The current at each end of the line is monitored by current transformers connected to local 87 relays, which makes the differential current protection zone cover the entire length of the transmission line. In order for this protection scheme to work, the two local 87 relays must somehow communicate with one another to continuously compare measured current values at both ends of the line. This is accomplished via a communication route between the two relays called a pilot channel. The term “pilot” is a general term in the field of protective relaying, referring to any form of data communication. If a significant difference in line current is detected (i.e. resulting from a fault anywhere along the length of the transmission line), both relays trip their respective circuit breakers and thereby de-energize the transmission line.
Pilot systems may take the form of an analog current or voltage “loop” circuit, a microwave radio link, a power-line carrier (PLC) link, a fiber-optic cable data link, or any other form of point-to-point data link allowing the relays to communicate data with each other. The details of pilot systems in protection schemes is complex and will not be treated in any detail here.
An interesting caveat when applying differential current protection to long lines is that the lines’ capacitive charging current may in some cases be substantial enough to trip an 87 relay that is configured too sensitively. One can visualize line-to-ground capacitance as a form of AC “ground fault” because any current taking that path to earth ground is current passing through one CT but not the other.
Not only is Kirchhoff’s Current Law unbounded with regard to distance, it is also unlimited with regard to the number of lines entering or exiting a node. This fact permits us to apply differential current protection to busses where multiple power lines and/or devices interconnect. An example of a high-voltage bus photographed at Grand Coulee Dam in Washington state appears here, connecting multiple three-phase transformer banks (each one fed by a hydroelectric generator):

Busses are typically constructed from flexible cable or rigid tube, suspended from ground by insulators. Faults may arise in a bus if an insulator “flashes over” (i.e. develops an electric arc from a bus conductor to ground), or if anything conductive happens to bridge between bus lines. As such, busses may be protected by the differential current principle just like any other electrical component or power line. The algebraic sum of all currents entering and exiting each phase of a bus should equal zero, and if it doesn’t it means the bus must be faulted.
A schematic diagram showing one bus with five different feeds reveals how differential current protection may be used to protect a bus with any number of lines. For simplicity’s sake the CT and 87 relay wiring is shown only for one phase on this three-phase bus. In any realistic bus differential protection circuit all three phases would be equipped with CTs and there would be three separate 87 “operating coil” elements, one for each phase:

Kirchhoff’s Current Law informs us that the algebraic sum of all currents at a node must equal zero. In this case the node in question is the sum of all conductors shown enclosed within the dotted blue protection zone outline. With all CTs possessing the same turns ratio and connected in parallel as shown, their combined secondary currents should all sum to a net value of zero amps through the 87 relay’s operate coil during normal operation. However, if a ground fault or a phase-to-phase fault happens to develop anywhere within the protection zone, the CT secondary currents will not sum to zero, causing the differential relay to pick up.
Another important concept in protective relaying is protection zone overlap. The philosophy here is that each protection zone’s size should be limited in order to avoid unnecessarily tripping any more sections of the power system than are necessary to isolate any fault, while leaving no component or conductor unprotected. The following single-line diagram shows how protection zones are configured to overlap each other at each circuit breaker where they connect:

For example, a fault in the upper transmission line belongs to that protection zone only, and will therefore only trip circuit breakers F and G, leaving the other transmission line and associated components to carry power from the generating station to the substation. Note how each circuit breaker in the above system falls within two protection zones. If fault happened to develop within breaker F, it would trip the breaker E in the upper generating station transformer zone as well as breaker G in the upper transmission line zone, isolating the failed breaker.
Differential protection zone overlap is accomplished by judicious placement of CTs on either side of a circuit breaker. Recall that the boundary of any differential current protection scheme is defined by the location of the CTs sensing current in and out of the node. Which CT a differential current relay connects to, therefore, defines how far the boundary of that relay’s protection zone will reach. We will take a closer look at the single-line diagram in order to explore this concept further, focusing in on the upper-left corner of the generating station and omitting all transformers and all but one generator as well as breakers C, D, and F for simplicity:

Here we see how zone overlap is achieved by connecting each differential relay to the far CT on each circuit breaker. If we instead chose to connect each 87 relay to the near CT, the two protection zones would not overlap, leaving every circuit breaker unprotected:

Perhaps the most interesting and challenging application of differential current protection is the protection of power transformers, which suffer many of the same vulnerabilities as generators and motors (e.g. winding faults). At first we might be tempted to connect CTs to every conductor entering and exiting a transformer, with 87 relays installed to compare these currents and trip if ever an imbalance were detected, just like protecting the individual windings in a generator. A single-phase transformer suffices to illustrate this concept, again omitting the restraint coils (RC) inside each of the differential relays for simplicity:

So long as each pair of CTs for each differential current relay were matched (i.e. same turns ratio), this protective relay circuitry would detect ground faults and winding-to-winding faults within the power transformer. However, one common transformer fault which would go undetected is a turn-to-turn fault within one of the windings. Such a fault would skew the turns ratio of the power transformer, but it would not upset the balance of current going in and coming out of any given winding and therefore would go undetected by the differential relays as shown.
A very clever way to improve differential current protection for a transformer is to have a single 87 relay compare primary and secondary currents for that transformer, thereby extending the zone of protection across both windings with just one relay:

One necessary condition for this strategy to work is to employ CTs with the necessary turns ratios to complement the power transformer’s turns ratio and give the 87 relay two equivalent currents to compare. For example, if our power transformer had a turns ratio of 20:1, our two CTs’ ratios must differ from each other by the same factor (e.g. a 50:5 CT on the low-current primary winding and a 1000:5 CT on the high-current secondary winding).
This differential current protection scheme works to detect common transformer faults in the following ways:
An interesting caveat to using differential current protection on a transformer is the phenomenon of inrush current which often happens when a transformer is initially energized. Inrush current happens when the residual magnetism in a transformer’s core from its last energized state happens to be substantial, and in the same polarity as the initial magnetization when first energized. The result is that the transformer core begins to magnetically saturate, the result being excess current in the primary winding that does not generate current in the secondary winding. Any differential current relay will naturally see this difference as a fault, and may trip power to the transformer unnecessarily.
A clever solution to the problem of false 87 relay tripping due to transformer inrush current is called harmonic restraint or harmonic blocking. Inrush currents tend to be asymmetrical when viewed on an oscilloscope, due to the bias of a pre-magnetized transformer core (i.e. the core’s magnetic field attains stronger peaks in one polarity than the other). This asymmetry results in significant second-harmonic content (e.g. 120 Hz in a 60 Hz power system) in the primary current and is therefore an accurate indicator of inrush. If an 87 relay is designed to detect this harmonic frequency it may be configured to provide additional restraint or even completely inhibit (“block”) its own tripping action until such time that the harmonics subside and the transformer stabilizes to normal operation.
Differential current protection of three-phase transformers and transformer banks is a more complicated matter, and not simply because there are three of everything. Power transformers are often wired with their primary and secondary sides in different configurations (e.g. Wye-Delta or Delta-Wye). Thus, the currents entering and exiting a power transformer may not be in-phase with each other, and in such cases cannot be compared directly against each other for differential current protection. Consider this example, where the primary winding is a Wye and the secondary winding is a Delta. For simplicity’s sake we will consider a transformer with equal numbers of turns on every winding, such that each primary/secondary coil pair has a 1:1 turns ratio. Furthermore, we will label each of the primary phase currents as \(I_A\), \(I_B\), and \(I_C\):

Since the secondary windings are Delta-connected, the secondary lines carry currents equal to \(I_A - I_C\), \(I_B - I_A\), and \(I_C - I_B\), respectively as declared by Kirchhoff’s Current Law at each of the Delta winding nodes. The result is that each secondary line current is \(\sqrt{3}\) times larger and lags 30\(^{o}\) behind each corresponding primary line current, as shown by the phasor diagrams. This 30\(^{o}\) phase shift means we cannot simply connect CT pairs together to a common 87 relay as we could in the single-phase transformer example. In order to compensate for the 30\(^{o}\) phase shift imparted by the power transformer, we must connect the CTs themselves in a complementary Delta-Wye configuration such that the 87 relays will be able to compare in-phase currents from primary and secondary sides of the power transformer.
In this schematic diagram we see how primary and secondary CTs need to be connected (CTs on the Wye side of the power transformer are Delta-connected, while CTs on the Delta side of the transformer are Wye-connected) to provide a matching 30\(^{o}\) phase shift. The currents generated by each CT secondary winding are labeled with lower-case letters (\(i\) rather than \(I\)) in order to represent their smaller values:

Note how each current entering an 87 relay’s restraint coil (RC) exits out the other restraint coil with the same mathematical expression, indicating equal current values. This will be true so long as all CT ratios are correct and currents into and out of the power transformer correspond properly to each other.
If the power transformer windings happen to have 1:1 turns ratios as is the case in this demonstration circuit, the secondary line currents will be larger than the primary line currents by a factor of \(\sqrt{3}\), owing to the fact that the primary windings are Wye-connected (winding currents same as line currents) while the secondary windings are Delta-connected (winding currents combine to make larger line currents). This means each of the secondary CTs will see a greater line current than each of the corresponding primary CTs. However, given the fact that the CTs on the primary side of the power transformer have their secondary windings Delta-connected, the actual amount of current they send to the 87 relay coils will be the same as the amount of current sent to the 87 relay by the other CTs, given equal CT ratios all around.
If the power transformer windings have turns ratios other than 1:1, the CTs installed on the primary and secondary lines will likely have differing ratios as well. It is unlikely that the CTs will exhibit precisely complementary ratios to the power transformer’s internal winding ratios, which means when these CTs are connected to 87 relays their output currents will not match in magnitude. Legacy electromechanical 87 relays were equipped with “taps” which could be set at different ratios to equalize the CT currents to within a few percent of agreement with each other. Modern digital 87 relays are able to do a much better job of matching primary-side and secondary-side CT outputs because they may be programmed with arbitrary correction factors. As you can see, care must be taken when connecting transformer CTs to differential current relays in order to ensure primary and secondary current values match in phase and magnitude.
It should be noted that the 30 degree phase shift between primary and secondary windings of the power transformer previously shown is actually a standard specified by the IEEE. The IEEE standard C57.12.00-2010 (“IEEE Standard for General Requirements for Liquid-Immersed Distribution, Power, and Regulating Transformers”) states that transformers having wye-wye or delta-delta winding configurations shall exhibit 0\(^{o}\) phase shift from input to output, but transformers having wye-delta or delta-wye winding configurations shall exhibit 30\(^{o}\) phase shift between primary and secondary sides with the lower-voltage side of the transformer lagging.
Modern digital 87 relays offer “CT compensation” which may be used in lieu of complementary connections to correct for the phase shift of a Wye-Delta power transformer, as well as correct for CT ratios that are not ideally matched. Rather than carefully connect the secondary windings of all CTs in such a manner that the primary- and secondary-side phase angles and current values match for all normal transformer operating conditions, we may connect the CTs as we see fit (typically in a Wye configuration on both827 sides, for simplicity) and let the relay mathematically match angles and magnitudes. This digital alternative, of course, requires careful attention to relay settings in order to work.
REVIEW:
If you are interested in more content about electrical power control systems, check out these calculators:
Related textbook pages:
Related Technical Articles: