What Exactly is a Voltage Drop?
Often the concept of voltage drop or voltage difference in circuits is taught without much explanation as to how or why volts drop. This article explores volts, including characteristics and the Laws that govern them.
The most common type of measurement in live circuit troubleshooting is the voltage drop — or voltage difference — between two points in a circuit. We use those two synonymous terms freely with a basic understanding of how the measurements point toward certain failures. However, the concept of ‘losing’ or ‘dropping’ voltage when passing through devices and loads can be a bit confusing.
After nearly 10 years as a professor of electronics and control systems, I always felt that I had a reasonable grasp of the fundamental concepts of these fields. But then I would sometimes be faced with a question that would humble my ego while illustrating how important it can be to realize how the circuits behave the way they do. Without this deep understanding, we are left to simply taking for granted that volts, amps, ohms, and watts behave the way we have been taught.
Voltage measurements in a live circuit can point to certain behaviors and failures, and as long as the work is done safely, the voltage can provide nearly everything a technician will need to know without harming the circuit under test. As an added bonus, the test tools (voltmeters) are very inexpensive.
We often teach the concept of a ‘voltage drop’ or ‘voltage difference’ in a circuit without much explanation of how or why the volts are dropping. Yet the daily task of an electrical technician is to use the two leads of the voltmeter to locate a problem.

Figure 1. Technicians use voltmeters regularly to find problems related to voltage drop.
First, What is a Volt?
In order to explain a loss or reduction in voltage, we first need to define a volt and where it comes from.
A volt is essentially the amount of potential energy between two points in a circuit with a charge passing through them. This ratio looks like this:

This fraction indicates some interesting observations:
- Two points must be examined in order to determine the volts. These two points may be microscopically close to each other or they could be across the county, but there is no voltage without two points. This is why we always say “voltage across, between, or difference.” It also explains why a voltmeter must have two leads.
- If the potential to use or convert the energy is greater, the voltage will be greater. Less energy potential means fewer volts.
- The charge traveling between the points relates to the current. This potential energy means that the charge must be ABLE to travel — voltage can still be present even if there is no current traveling. Since it is on the bottom of the fraction, this is an inverse ratio. If you expect to convert energy with only a tiny amount of charge motion, the voltage must be large. If the charge is very large, the voltage will be small.
How Can You ‘Lose’ Voltage?
The most important factor to consider is the potential energy difference at the top of the fraction. Every motion of electrons consumes some of that potential energy. It may be further converted into mechanical motion, heat, light, sound, or a number of other energy types.
In a load device such as an incandescent light, much of that potential energy is lost beyond the simple motion of electrons — the light also generates light and heat. Therefore, the ‘voltage’ from one side of the light to the other will be the resulting loss of potential in that motion, light, and heat. So it will have a large voltage drop from one side to the other.
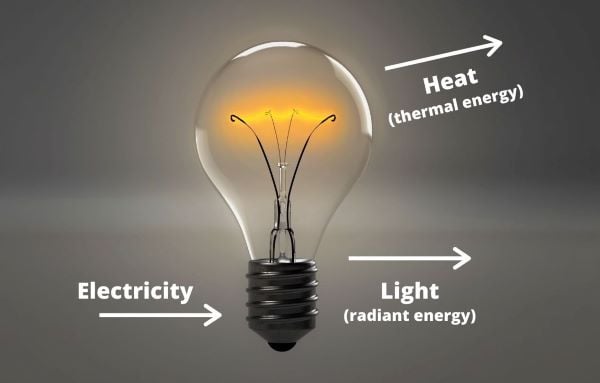
Figure 2. A lightbulb receiving electricity (voltage) converts energy into light and heat.
In contrast, a properly gauged wire generates very little heat, so the only loss of voltage comes from the motion of the electrons.
A large motor requires a ton of energy, so we expect a lot of voltage. If we wish to reduce the voltage required while still providing the required energy, then the charge motion (current) must be increased.
Typically, it’s more expensive to increase the current since you need larger wires, larger conduits, and larger breakers and fuses — lots of expense. Therefore, it is likely to have large loads driven with large voltages, not large currents.
Why Does the Sum of All Voltages Equal Zero?
The popular equation of Kirchhoff's Voltage Law states that all voltage drops in a circuit must add up to zero. In other words, whatever voltage you supply into the circuit will be consumed by the devices and conductors in the circuit.
When we provide voltage from a power supply, this means we are supplying the potential to convert a certain amount of energy with a certain amount of charge motion. When the power supply is connected to a continuous circuit, one of two scenarios will occur.
Scenario One
If the supply is capable of providing a high current (such as a car battery or mains AC supply) then both the energy consumed AND the charge motion (current) will increase until they cannot increase further, or in other words, until the voltage used by the circuit reaches the voltage of the supply.

Figure 3. Car batteries are capable of providing a high current, so the energy consumed and the current increase until the voltage used by the circuit reaches the voltage of the supply.
Hopefully, the circuit has been connected to the right supply voltage, and every device is converting the right amount of energy with the right amount of current.
If the resistance of the circuit is too small, the charge motion (current) will increase, and so will the energy consumed. This may damage the load devices. If the resistance is nearly zero, a short-circuit, then the current and energy will both climb very high, and the circuit will likely smoke and burn up.
Scenario Two
If the supply cannot reach a high current (such as a AA battery or small coin-cell battery), then the above scenario is correct until the resistance begins to decrease. The charge motion will try to climb, but the battery cannot provide such current. Since the current no longer increases, neither does the energy consumption, and the voltage maxes out below the rated voltage.

Figure 4. Coin-cell batteries can only provide a certain amount of current. Without the current and energy increasing, the voltage maxes out below the rated voltage. Image courtesy of Gerhard H Wrodnigg. [CC BY-SA 2.5]
This is called the ‘loading effect’ of a circuit. When current is demanded, the supply voltage will drop. If a short-circuit is reached, expect the supply voltage to drop dramatically, but it depends on the capacity of the supply.
So we can say that Kirchoff’s Voltage Law is always true, but we must consider what will happen to different kinds of supplies when the resistance of the circuit is reduced. The sum of all voltages will still equal zero, but we might find that the load voltage will drop as we consume more energy — in some supplies more than others.






