Technical Article

What is Proportional Gain?

February 13, 2023 by David Peterson

This article discusses the meaning and effects of proportional gain in a controlled system such as motion, temperature, and fluid flow.

In a controlled system, feedback is important to ensure that a required action has happened. If a sensor can read information about the current operating status of the equipment, the control system must calculate the required output action needed to reach the next step, which repeats until the goal has been reached.

The controller can be programmed to send an output signal proportional to the current distance from the goal point—a large output if far away, a small output as the goal gets closer. This is proportional gain.

red stoplight is like a set point

Figure 1. A red stoplight at an instersection is like a set point/goal position. Image used courtesy of Canva

The Problem with On/Off (Bang Bang) Control

Imagine you are in your car, driving down the highway. The speed limit is 55, so of course you are doing 60, when far ahead, you see a red stoplight at an intersection. Since you are the car's controller, you immediately recognize this as the ‘set point’ (SP), or goal position, which you must reach and come to a stop at.

Would you continue driving 60 until you cross the white line at the intersection and then instantly remove your foot from the gas pedal? Of course not! You know what would happen if you waited until reaching the intersection to remove the throttle. The car’s momentum would carry you far past the intersection, most likely leading to a tragic collision.

This example illustrates the most basic form of feedback control, which uses a discrete signal (on/off only) to alert the controller when the SP is reached. In this type of control system, the output is driven at 100% until the SP is reached, then the output is reduced to 0%. If the system has a good deal of inertia, the momentum will carry it beyond the SP in a condition called overshoot.

To connect this to a real-life process, imagine a hydraulic cylinder controlled with an analog 0-10 V valve. The movement must be very fast and reach the SP with as little overshoot as possible. A magnetic sensor on the outside of the cylinder reacts when the cylinder reaches the set position. A fully open valve will drive the cylinder motion quickly but cannot suddenly stop when the magnetic sensor is tripped.

Finding more precise measuring sensors in nearly every control system setting is imperative. In this hydraulic cylinder, an internal Temposonic sensor may be installed, or perhaps it’s an encoder for RPM measurements, a pressure gauge for vacuum systems, or a temperature sensor for systems that rely on heating liquids or gasses. In all of these cases, an analog information source can provide not just an alert of reaching an SP but also a known position the entire time the system is in motion—even if it shoots beyond the set point.

Proportional Response

If we return to the analogy of the car, the reality is that a good driver will observe how close the intersection is getting and will begin to reduce throttle while the intersection is still a long distance away. As it gets closer, the throttle will continue to reduce.

Even if a driver is unaware of the mental math, there is somewhat of a calculation happening based on the difference between the car’s current location and the location of the goal position.

This difference between the current value of the system, often called the process variable (PV), and the goal position SP is referred to as ‘error’.

$$Error = SP-PV$$

Conditions of Error

There are three possible conditions of error.

A positive error value means the system must be propelled in a positive direction to reach the SP. Most likely, the error is positive because the SP has yet to be reached. It may also have a positive error value when the SP has been overshot, then overcorrected and overshot once more in a process called ‘oscillation.’

An error of 0 is only achieved if the current PV lands perfectly on the SP. This, of course, is the ultimate goal of the control system.

A negative error occurs when either the system has overshot the SP or if the SP has been adjusted to a lower value and the system must be returned to a matching value.

Based on these three conditions, we can see that the error is the greatest as soon as a change is ordered. At the beginning of a shift or a change in product type, which requires a large SP adjustment, the error will be at a maximum, and the output signal should also be at a maximum to meet it.

We can take the raw error, defined above, and multiply it by a predetermined number called the ‘proportional gain’ which has the abbreviation Kp:

$$Output~Signal = Error \times (K_p)$$

This Kp value is a unitless multiplying number ranging from small decimals to large values. This is the definition of a direct proportion from algebra which multiplies an input value by a proportional constant to yield an output. This proportional constant is simply the Kp.

Effect of Proportional Gain

For a low value of Kp, the output signal will be smaller. This means the system will be slower to respond, perhaps seeming a bit sluggish. With a low Kp value, it will also reach a point where the output signal is so small that it can’t overcome the opposing force of the system and basically stall—never quite reaching the SP. This is called a 'steady-state error' since there is still a bit of error once the system stops responding and becomes steady.

On the positive side, a low Kp value can ensure minimal system overshoot since the output is going quite slowly by the time it reaches the SP.

Naturally, when the Kp is increased, the opposite effect is true from what is listed above.

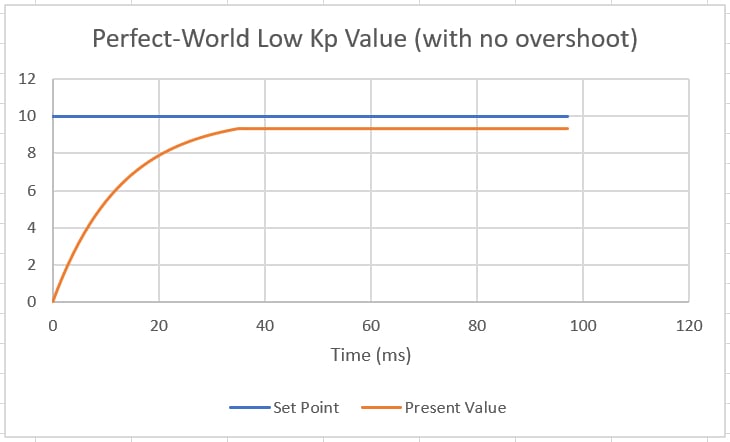
Figure 2. A graph of a system response with only a low proportional gain value of 0.075. Note the response time is quite slow, and the system fails to reach the final SP—however, it will not overshoot the SP.

Figure 3. A graph of a system response with only a high proportional gain value of 0.3. Note the quick time to rise and settle right on the SP line. In the real world, there would be some sort of inertia leading to overshoot—this is simply a simulation of a system response.

	Low $K_p$ Value	High $K_p$ Value
System Response Time (speed)	Worse	Better
Overshoot	Better	Worse
Steady-State Error	Worse	Better

Improvements in Proportional Control

The effects of proportional control can never lead to a perfect system that responds instantly, with zero overshoot and zero steady-state error. Adjustments in the value will lead to compromises that simply must be accepted. The further addition of 'integral' and 'derivative' control terms can greatly improve the system response and error.